Question

5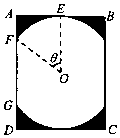．某景区修建一栋复古建筑，其窗户设计如图所示．圆O的圆心与矩形ABCD对角线的交点重合，且圆与矩形上下两边相切（E为上切点），与左右两边相交（F，G为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m且$\frac{AB}{AD}$≥$\frac{1}{2}$，设∠EOF=θ，透光区域的面积为S．
（1）求S关于θ的函数关系式，并求出定义域；
（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好．当该比值最大时，求边AB的长度．

Answer 1

分析 （1）过点O作OH⊥FG于H，写出透光面积S关于θ的解析式S，并求出θ的取值范围；
（2）计算透光区域与矩形窗面的面积比值，构造函数，利用导数判断函数的单调性，
求出比值最大时对应边AB的长度．

解答 解：（1）过点O作OH⊥FG于H，∴∠OFH=∠EOF=θ；
又OH=OFsinθ=sinθ，
FH=OFcosθ=cosθ，
∴S=4S_△OFH+4S_阴影OEF=2sinθcosθ+4×$\frac{1}{2}$θ=sin2θ+2θ；
∵$\frac{AB}{AD}$≥$\frac{1}{2}$，∴sinθ≥$\frac{1}{2}$，∴θ∈[$\frac{π}{6}$，$\frac{π}{2}$）；
∴S关于θ的函数关系式为S=sin2θ+2θ，θ∈[$\frac{π}{6}$，$\frac{π}{2}$）；

（2）由S_矩形=AD•AB=2×2sinθ=4sinθ，
∴$\frac{2sinθcosθ+2θ}{4sinθ}$=$\frac{cosθ}{2}$+$\frac{θ}{2sinθ}$，
设f（θ）=$\frac{cosθ}{2}$+$\frac{θ}{2sinθ}$，θ∈[$\frac{π}{6}$，$\frac{π}{2}$），
则f′（θ）=-$\frac{1}{2}$sinθ+$\frac{sinθ-θcosθ}{{2sin}^{2}θ}$
=$\frac{sinθ-θcosθ{-sin}^{3}θ}{{2sin}^{2}θ}$
=$\frac{sin{θcos}^{2}θ-θcosθ}{{2sin}^{2}θ}$
=$\frac{cosθ（\frac{1}{2}sin2θ-θ）}{{2sin}^{2}θ}$；
∵$\frac{π}{6}$≤θ＜$\frac{π}{2}$，∴$\frac{1}{2}$sin2θ≤$\frac{1}{2}$，
∴$\frac{1}{2}$sin2θ-θ＜0，
∴f′（θ）＜0，
∴f（θ）在θ∈[$\frac{π}{6}$，$\frac{π}{2}$）上是单调减函数；
∴当θ=$\frac{π}{6}$时f（θ）取得最大值为$\frac{π}{6}$+$\frac{\sqrt{3}}{4}$，
此时AB=2sinθ=1（m）；
∴S关于θ的函数为S=sin2θ+2θ，θ∈[$\frac{π}{6}$，$\frac{π}{2}$）；所求AB的长度为1m．

点评 本题考查了三角函数模型的应用问题，也考查了三角恒等变换以及三角函数最值的应用问题，是综合题．