题目内容
已知x，y满足约束条件
，设M，m分别为目标函数z=3x+5y的最大、最小值，则M-m为（ ）
|
| A、9 | B、11 | C、17 | D、28 |
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，根据z的几何意义，利用数形结合即可得到最大值和最小值．
解答：
解：不等式组对应的平面区域如图：
由z=3x+5y得y=-
x+
，
平移直线y=-
x+
，则由图象可知当直线y=-
x+
经过点A时直线y=-
x+
的截距最大，
此时z最大，当经过点B时，直线的截距最小，此时z最小．
由
解得
，即A（
，
），
此时M=z=3×
+5×
=17，
由
，解得
，即B（-2，-1），
此时m=3×（-2）+5×（-1）=-11，
∴M-m=17-（-11）=28，
故选：D
由z=3x+5y得y=-
| 3 |
| 5 |
| z |
| 5 |
平移直线y=-
| 3 |
| 5 |
| z |
| 5 |
| 3 |
| 5 |
| z |
| 5 |
| 3 |
| 5 |
| z |
| 5 |
此时z最大，当经过点B时，直线的截距最小，此时z最小．
由
|
|
| 3 |
| 2 |
| 5 |
| 2 |
此时M=z=3×
| 3 |
| 2 |
| 5 |
| 2 |
由
|
|
此时m=3×（-2）+5×（-1）=-11，
∴M-m=17-（-11）=28，
故选：D
点评：本题主要考查线性规划的应用，根据z的几何意义，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
已知直线l与双曲线C交于A，B两点（A，B不在同一支上），F1，F2为双曲线的两个焦点，则F1，F2在（ ）
| A、以A，B为焦点的双曲线上 |
| B、以A，B为焦点的椭圆上 |
| C、以A，B为直径两端点的圆上 |
| D、以上说法均不正确 |
执行如图的程序框图．若输入n=7，则输出的值为（ ）
| A、2 | B、3 | C、4 | D、5 |
复数
（i是虚数单位）化简的结果是（ ）
| 1-i |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
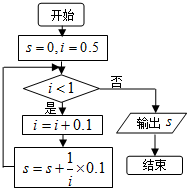
执行如图的程序框图，则输出的S值等于（ ）
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
如图，焦距为2的椭圆E的两个顶点分别为A和B，且
已知正三棱柱ABC-A1B1C的底面边长为4cm，高为7cm，则当一质点自点A出发，沿着三棱柱的侧面绕行两周到达点A1的路程最短时，质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为