已知正三棱柱ABC-A1B1C的底面边长为4cm.高为7cm.则当一质点自点A出发.沿着三棱柱的侧面绕行两周到达点A1的路程最短时.质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为．题目和参考答案——青夏教育精英家教网—

题目内容

已知正三棱柱ABC-A₁B₁C的底面边长为4cm，高为7cm，则当一质点自点A出发，沿着三棱柱的侧面绕行两周到达点A₁的路程最短时，质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为

．

考点：多面体和旋转体表面上的最短距离问题

专题：空间角

分析：由题意，∠DAB为质点沿着侧面的前进方向所在直线与底面ABC所成角．将正三棱柱ABC-A₁B₁C₁沿侧棱展开，再拼接一次，求出BD，AD，即可求出质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值．

解答：

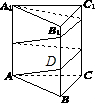解：由题意，∠DAB为质点沿着侧面的前进方向所在直线与底面ABC所成角．
将正三棱柱ABC-A₁B₁C₁沿侧棱展开，再拼接一次，其侧面展开图如图所示，

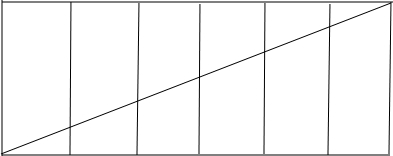
在展开图中，可知BD=

cm，∴AD=

16+(

cm，
∴cos∠DAB=

．
故答案为：

．

点评：本题考查棱柱的结构特征，空间想象能力，几何体的展开与折叠，体现了转化（空间问题转化为平面问题，化曲为直）的思想方法．

练习册系列答案

相关题目

，设M，m分别为目标函数z=3x+5y的最大、最小值，则M-m为（　　）

．
（1）若点P（2，1）在椭圆上，求椭圆的方程；
（2）若存在过点A（1，0）的直线l，使点C（2，0）关于直线l的对称点在椭圆上，求椭圆的焦距的取值范围．

如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，且AD∥BC，∠ABC=∠PAD=90°，侧面PAD⊥底面ABCD．若PA=AB=BC=

AD．
（Ⅰ）求证：CD⊥PC；
（Ⅱ）求二面角A-PD-C的余弦值．

某班有班干部6人，其中有女同学4人，所有班干部中只有男同学甲和女同学乙参加过社区服务，今抽调3名班干部组成青年志愿者活动小组到社区服务，小组中必须有男有女，且甲、乙两人至少有一人参加，那么不同的选派方法共有

种．

已知数列{a_n}满足a₁=100，a_n+1-a_n=2n，则

的最小值

．

已知长方体ABCD-A′B′C′D′的长宽高分别为a，b，c，（a＞b＞c），一只蚂蚁沿一个长方体ABCD-A′B′C′D′的表面爬行从A到C′的最短距离为

．

已知O为△ABC的外心，AB=2a，AC=

（a＞0），∠BAC=120°．若

=α

+β

(α，β∈R)，则α+β的最小值为（　　）

已知f（x）是R上的奇函数，且f（x+2）=-f（x），当-1≤x≤1时，f（x）=x³．求x∈R时f（x）的解析式．

试题分类