题目内容
19.已知正数x,y满足$\frac{4x-y}{4x+3y}$=4xy,那么y的最大值为$\frac{1}{3}$.分析 正数x,y满足$\frac{4x-y}{4x+3y}$=4xy,化为:16yx2+(12y2-4)x+y=0,关于x的一元二次方程有正实数根,利用方程与判别式的关系、根与系数的关系即可得出.
解答 解:正数x,y满足$\frac{4x-y}{4x+3y}$=4xy,化为:16yx2+(12y2-4)x+y=0,
关于x的一元二次方程有正实数根,
∴$\left\{\begin{array}{l}{-\frac{12{y}^{2}-4}{16y}>0}\\{△=(12{y}^{2}-4)^{2}-64{y}^{2}≥0}\end{array}\right.$,又y>0,
解得$y≤\frac{1}{3}$.
那么y的最大值为$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 本题考查了一元二次方程有正实数根与判别式及其根与系数的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.若三棱锥P-ABC中,AB=AC=1,AB⊥AC,PA⊥平面ABC,且直线PA与平面PBC所成角的正切值为$\frac{1}{2}$,则三棱锥P-ABC的外接球的表面积为( )
| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
9.将一个总数为A、B、C三层,其个体数之比为5:3:2.若用分层抽样方法抽取容量为100的样本,则应从C中抽取( )个个体.
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
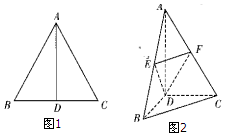 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.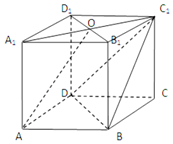 如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=2,∠BAD=60°;
如图,在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=2,∠BAD=60°;