题目内容
7．在棱长为3的正方体内任取一点P，则点P到正方体各个面的距离都不小于1的概率为$\frac{1}{27}$．分析 根据点P与正方体各表面的距离都大于1，则所在的区域为以棱长为1的正方体内，则概率为两正方体的体积之比．
解答 解：符合条件的点P落在棱长为1的正方体内，
根据几何概型的概率计算公式得P=$\frac{1}{{3}^{3}}$=$\frac{1}{27}$，
故答案为：$\frac{1}{27}$．
点评 本题主要考查几何概型中的体积类型，基本方法是：分别求得构成事件A的区域体积和试验的全部结果所构成的区域体积，两者求比值，即为概率．
练习册系列答案
名校课堂系列答案
相关题目
5．在△ABC中，若b2+c2=a2-bc，则∠A=（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 120° |
15．若双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线的倾斜角是直线l：x-2y+1=0倾斜角的两倍，则双曲线的离心率为（ ）
| A． | $\frac{5}{3}$ | B． | $\frac{{\sqrt{7}}}{3}$ | C． | $\frac{5}{4}$ | D． | $\frac{4}{3}$ |
12．已知{an}是公差为1的等差数列，Sn为{an}的前n项和，若S6=4S3，则a10=（ ）
| A． | $\frac{17}{2}$ | B． | $\frac{19}{2}$ | C． | $\frac{9}{10}$ | D． | $\frac{8}{9}$ |
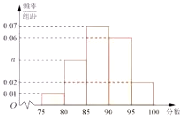某地区有800名学员参加交通法规考试，考试成绩的频率分布直方图如图所示，其中成绩分组区间是：[75，80），[80，85），[85，90），[90，95），[95，100]，规定90分及以上为合格：
17．若f（x）=sinα-cosx，则f′（x）等于（ ）
| A． | 2sinα+cosx | B． | cosα+sinx | C． | cosx | D． | sinx |