题目内容
7.已知f(x)=2x2+2bx+c,且f(0)=-6,f(x)的最小值为-8,求f(x)的单调增区间.分析 求出c的值,根据f(x)的最小值是-8,求出b=2或-2,从而求出f(x)的递增区间即可.
解答 解:∵f(0)=-6,∴c=-6,
∴f(x)=2x2+2bx-6,
∵f(x)的最小值为-8,
∴$\frac{4•2•(-6)-{4b}^{2}}{8}=-8$,
解得:b=±2,
b=2时,对称轴x=-1,f(x)在(-1,+∞)递增,
b=-2时,对称轴x=1,f(x)在(1,+∞)递增.
点评 不同考查了二次函数的性质,考查函数的单调性问题,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.过抛物线y2=4x的焦点F作直线l,与抛物线分别交于A、B两点(A点在第一象限),若S△AOB=3S△FOB,则直线l的斜率k=( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 3 |
12.已知抛物线C:y2=-8x的交点为F,直线l:x=1,点A是l上一动点,直线AF与抛物线C的一个交点为B,若$\overrightarrow{FA}$=-$\overrightarrow{FB}$,则|AB|=( )
| A. | 20 | B. | 14 | C. | 10 | D. | 5 |
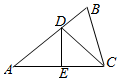 如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.
如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.