题目内容
12.已知抛物线C:y2=-8x的交点为F,直线l:x=1,点A是l上一动点,直线AF与抛物线C的一个交点为B,若$\overrightarrow{FA}$=-$\overrightarrow{FB}$,则|AB|=( )| A. | 20 | B. | 14 | C. | 10 | D. | 5 |
分析 设A(-1,a),B(m,n),且n2=-8m,利用向量共线的坐标表示,由$\overrightarrow{FA}$=-$\overrightarrow{FB}$,确定A,B的坐标,即可求得.
解答 解:由抛物线C:y2=-8x,可得F(-2,0),
设A(1,a),B(m,n),且n2=-8m,
∵$\overrightarrow{FA}$=-$\overrightarrow{FB}$,
∴1+2=-(m+2),∴m=-5,
∴n=±2$\sqrt{10}$,
∵a=-n,∴a=±2$\sqrt{10}$,
∴|AB|=$\sqrt{(1-m)^{2}+(a-n)^{2}}$=14.
故选:B.
点评 本题考查抛物线的性质,考查向量知识的运用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
1.若命题p:?x∈R,不等式x2-2$\sqrt{2}$x+a>0恒成立,命题q:?x∈R,不等式|x-1|+|x+1|>a恒成立,则命题¬p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
 如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.
如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.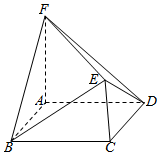 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.