题目内容
18.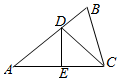 如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.
如图,设△ABC的个内角A、B、C对应的三条边分别为a、b、c,且角A、B、C成等差数列,a=2,线段AC的垂直平分线分别交线段AB、AC于D、E两点.(1)若△BCD的面积为$\frac{\sqrt{3}}{3}$,求线段CD的长;
(2)若DE=$\frac{\sqrt{6}}{2}$,求角A的值.
分析 (1)先根据三角形的内角A,B,C成等差数列,求出B的度数,再根据三角的面积公式求出BD,再根据余弦定理即可求出,
(2)根据垂直平分线的性质得到AC=2AE=$\frac{\sqrt{6}}{tanA}$,再根据正弦定理,即可求出答案.
解答 解:(1)三角形的内角A,B,C成等差数列,
则有2B=A+C.又A+B+C=180°,
∴B=60°,
∵△BCD的面积为$\frac{\sqrt{3}}{3}$,a=2
∴$\frac{1}{2}$BD•BC•sin60°=$\frac{\sqrt{3}}{3}$,
∴BD=$\frac{2}{3}$,
由余弦定理,CD2=BD2+BC2+2BD•BC•cos60°=$\frac{4}{9}$+4+2×$\frac{2}{3}$×2×$\frac{1}{2}$=$\frac{4×13}{9}$,
∴CD=$\frac{2\sqrt{13}}{3}$,
(2)∵线段AC的垂直平分线分别交线段AB、AC于D、E两点,DE=$\frac{\sqrt{6}}{2}$,
∴AE=$\frac{DE}{tanA}$,
∴AC=2AE=2×$\frac{\frac{\sqrt{6}}{2}}{tanA}$=$\frac{\sqrt{6}}{tanA}$,
由正弦定理可得$\frac{BC}{sinA}$=$\frac{AC}{sinB}$,
即$\frac{2}{sinA}$=$\frac{\frac{\sqrt{6}}{tanA}}{sin60°}$,
∴cosA=$\frac{\sqrt{2}}{2}$,
∵0<A<180°,
∴A=45°
点评 本题主要考察了正弦定理余弦定理三角形的面积公式以及等差数列的性质,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
8.“m>n>0”是“曲线mx2+ny2=1为焦点在x轴上的椭圆”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.函数y=x2+2x-1的顶点坐标是( )
| A. | ($\frac{1}{10}$,2) | B. | ($\frac{1}{10}$,-2) | C. | (-1,-2) | D. | (1,-2) |