题目内容
12．随机变量X的分布列如下：| X | -1 | 0 | 1 |
| P | a | b | c |
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
分析 由随机变量X的分布列的性质得a+b+c=1，且a，b，c∈[0，1]．由a，b，c成等差数列，得2b=a+c，从而能求出P（|x|=1）=P（X=-1）+P（X=1）的值．
解答 解：∵随机变量X的分布列如下：
| X | -1 | 0 | 1 |
| P | a | b | c |
∵a，b，c成等差数列，
∴2b=a+c，②
联立①②，得b=$\frac{1}{3}$，a+c=$\frac{2}{3}$，
∴P（|x|=1）=P（X=-1）+P（X=1）=a+c=$\frac{2}{3}$．
故选：D．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意随机变量的分布列和等差数列的性质的合理运用．
练习册系列答案
相关题目
3．
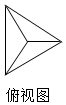一个正四面体的体积为$\frac{2\sqrt{2}}{3}$，它的三视图中的俯视图如图所示（其中三个小三角形全等），侧视图是一个三角形，则这个三角形的面积是（ ）
一个正四面体的体积为$\frac{2\sqrt{2}}{3}$，它的三视图中的俯视图如图所示（其中三个小三角形全等），侧视图是一个三角形，则这个三角形的面积是（ ）| A． | $\frac{\sqrt{6}}{3}$ | B． | $\frac{2\sqrt{6}}{3}$ | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\sqrt{3}$ |