题目内容
1.求下列各式的值:(1)cos105°
(2)cos(-$\frac{25π}{12}$)
分析 (1)直接利用两角和与差的三角函数求解即可.
(2)利用诱导公式化简,以及两角和与差的余弦函数求解即可.
解答 解:(1)cos105°=cos(45°+60°)=cos45°cos60°-sin45°sin60°=$\frac{\sqrt{2}-\sqrt{6}}{4}$
(2)cos(-$\frac{25π}{12}$)=cos(2π$+\frac{π}{12}$)=cos($\frac{π}{4}-\frac{π}{6}$)=cos$\frac{π}{4}$cos$\frac{π}{6}$+sin$\frac{π}{4}$sin$\frac{π}{6}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
点评 本题考查两角和与差的三角函数以及诱导公式的应用,三角函数求值,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.随机变量X的分布列如下:
其中a,b,c成等差数列,则P(|x|=1)=( )
| X | -1 | 0 | 1 |
| P | a | b | c |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
6.下列说法正确的是( )
| A. | y=sinx在第三象限内是增函数 | B. | 函数y=sinx(x∈R)的值域是(-1,1) | ||
| C. | y=cosx在x=2kπ(k∈Z)时取值最大 | D. | y=tanx在整个定义域内都是增函数 |
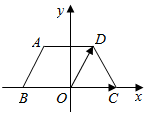 如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.
如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.