题目内容
7．求证：$\frac{1+sin2θ}{sinθ+cosθ}$=sinθ+cosθ．分析 利用倍角公式及同角三角函数基本关系式把等式左边化为完全平方式，约分后得答案．
解答 证明：$\frac{1+sin2θ}{sinθ+cosθ}$=$\frac{si{n}^{2}θ+2sinθcosθ+co{s}^{2}θ}{sinθ+cosθ}=\frac{（sinθ+cosθ）^{2}}{sinθ+cosθ}$=sinθ+cosθ．
点评 本题考查三角函数恒等式的证明，考查倍角公式及同角三角函数基本关系式的应用，是基础题．
练习册系列答案
相关题目
18．若命题：“?x∈R，x2-2ax+a≤0”为假命题，则$\frac{{2{a^2}+1}}{a}$的最小值是（ ）
| A． | $2\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $2\sqrt{3}$ | D． | $\sqrt{3}$ |
15．设i为虚数单位，则i2014=（ ）
| A． | 1 | B． | i | C． | -1 | D． | -i |
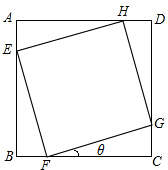如图所示，某住宅小区内有一正方形草地ABCD，现欲在其中修建一个正方形花坛EFGH，若已知花坛面积为正方形草地面积的$\frac{2}{3}$，则θ=arctan（2-$\sqrt{3}$）．
12．随机变量X的分布列如下：
其中a，b，c成等差数列，则P（|x|=1）=（ ）
| X | -1 | 0 | 1 |
| P | a | b | c |
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
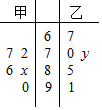一次数学考试后，某老师从自己带的两个班级中各抽取5人，记录他们的考试成绩，得到如图所示的茎叶图，已知甲班5名同学成绩的平均数为81，乙班5名同学的中位数为73，则x-y的值为（ ）