题目内容
20.已知ω>0,函数f(x)=cos(ωx+$\frac{π}{3}$)的一条对称轴为x=$\frac{π}{3}$,一个对称中心为点($\frac{π}{12}$,0),则ω的最小值为2.分析 分别由对称轴和对称中心可得ω表达式,由ω>0综合可得.
解答 解:∵函数f(x)=cos(ωx+$\frac{π}{3}$)的一条对称轴为x=$\frac{π}{3}$,
∴ω•$\frac{π}{3}$+$\frac{π}{3}$=kπ,解得ω=3k-1,k∈Z;
由ω>0可知当k=1时,ω取最小值2.
又∵函数f(x)一个对称中心为点($\frac{π}{12}$,0),
∴ω•$\frac{π}{12}$+$\frac{π}{3}$=mπ+$\frac{π}{2}$,解得ω=12m+2,m∈Z;
由ω>0可知当m=0时,ω取最小值2.
综上可得ω的最小值为2
故答案为:2
点评 本题考查余弦函数的对称性,属基础题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
10.在复平面内,复数$\frac{2+i}{2i}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.设i为虚数单位,则i2014=( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
12.随机变量X的分布列如下:
其中a,b,c成等差数列,则P(|x|=1)=( )
| X | -1 | 0 | 1 |
| P | a | b | c |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
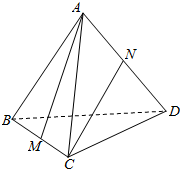 在正四面体(四个面都是正三角形的四面体是正四面体)中,M,N分别是BC和AD的中点,试作出异面直线AM与CN所成角.
在正四面体(四个面都是正三角形的四面体是正四面体)中,M,N分别是BC和AD的中点,试作出异面直线AM与CN所成角.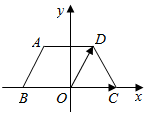 如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.
如图,在直角坐标平面内,等腰梯形ABCD的下底BC在x轴上,BC的中点是坐标原点0,已知AD=AB=DC=1,BC=2.