题目内容
11.已知正实数x,y满足4x2-2xy+y2=1,则2x+y的取值范围是(1,2];2x-y的取值范围是(-1,1).分析 令t=2x+y,则y=-2x+t,t>0,代入4x2-2xy+y2=1得12x2-6tx+t2-1=0,由△=36t2-48(t2-1)≥0,结合4x2+4xy+y2=1+6xy>1,即(2x+y)2>1,解关于2x+y的不等式可得2x+y的取值范围;
令t=2x-y,则y=2x-t,代入4x2-2xy+y2=1得:4x2-2tx+t2-1=0,由△=4t2-16(t2-1)≥0,结合4x2-4xy+y2=1-2xy<1,即(2x-y)2<1,解关于2x-y的不等式可得2x-y的取值范围;
解答 解:令t=2x+y,则y=-2x+t,t>0,
代入4x2-2xy+y2=1得:4x2-2x(-2x+t)+(-2x+t)2=1,
即12x2-6tx+t2-1=0,
由△=36t2-48(t2-1)≥0得:t∈[-2,2],
又由4x2+4xy+y2=1+6xy>1,即(2x+y)2>1,
解得:2x+y∈(1,+∞),
故2x+y∈(1,2],
同理令t=2x-y,则y=2x-t,
代入4x2-2xy+y2=1得:4x2-2x(2x-t)+(2x-t)2=1,
即4x2-2tx+t2-1=0,
由△=4t2-16(t2-1)≥0得:t∈[-$\frac{2\sqrt{3}}{3}$,$\frac{2\sqrt{3}}{3}$],
又由4x2-4xy+y2=1-2xy<1,即(2x-y)2<1,
解得:2x-y∈(-1,1),
故2x-y∈(-1,1),
故答案为:(1,2],(-1,1)
点评 本题考查了基本不等式的应用问题,也考查了不等式的解法与应用问题,是综合性题目

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.两个圆锥有公共底面,且两圆锥的顶点和底面圆周都在同一个球面上.若圆锥底面面积是球面面积的$\frac{3}{16}$,则这两个圆锥的体积之比为( )
| A. | 2:1 | B. | 5:2 | C. | 1:4 | D. | 3:1 |
2.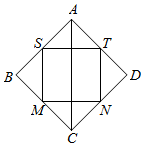 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
 如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )
如图,记正方形ABCD四条边的中点为S、M、N、T,连接四个中点得小正方形SMNT.将正方形ABCD、正方形SMNT绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1,V2,则V1:V2=( )| A. | 8:1 | B. | 2:1 | C. | 4:3 | D. | 8:3 |
19.设函数$f(x)=\left\{\begin{array}{l}3x-1,\;x<3\\{2^x},\;x≥3\end{array}\right.$,则满足f(f(a))=2f(a)的a取值范围是( )
| A. | $[{\frac{2}{3},\;\frac{4}{3}}]$ | B. | $[{\frac{2}{3},\;+∞})$ | C. | $[{\frac{4}{3},\;+∞})$ | D. | $[{\frac{4}{3},\;+∞}]∪\left\{{\frac{2}{3}}\right\}$ |
6.“0<a<3”是“双曲线$\frac{{x}^{2}}{a}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.己知tanx=2,则$\frac{5sinx-cosx}{2sinx+cosx}$=( )
| A. | $\frac{6}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{8}{5}$ | D. | $\frac{7}{5}$ |
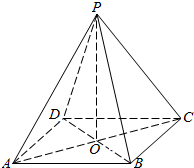 如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:
如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求: