题目内容
16.已知函数$f(x)=sin(x+\frac{π}{6})+sin(x-\frac{π}{6})+cosx+a$的最大值为1.(Ⅰ)求常数a的值;
(Ⅱ)若A为△ABC的内角,$A∈({0,\frac{π}{2}})$,$f(A)=\sqrt{3}-1$,△ABC的面积为$\sqrt{3}$,AB=$2\sqrt{3}$,求BC的长.
分析 (Ⅰ)由三角函数公式化简可得f(x)=2sin(x+$\frac{π}{6}$)+a由最大值为1可2+a=1,解方程可得;
(Ⅱ)由题意和(Ⅰ)可得$A=\frac{π}{6}$,由三角形的面积公式可得b=2,再由余弦定理可得.
解答 解:(Ⅰ)由三角函数公式化简可得:
f(x)=$\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx-$\frac{1}{2}$cosx+cosx+a
=$\sqrt{3}$sinx+cosx+a=2sin(x+$\frac{π}{6}$)+a
由最大值为1可2+a=1,解得a=-1,
∴$f(x)=2sin(x+\frac{π}{6})-1$;
(Ⅱ)由$f(A)=2sin(A+\frac{π}{6})-1=\sqrt{3}-1$,$A∈({0,\frac{π}{2}})$,得$A=\frac{π}{6}$,
∵$S=\frac{1}{2}bcsinA=\sqrt{3}$,∴b=2,∵a2=b2+c2-2bccosA=4,
∴a=2,即BC的长为2.
点评 本题考查正余弦定理解三角形,涉及三角形的面积公式,属基础题.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
6.已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有( )
| A. | 2 个 | B. | 3个 | C. | 4个 | D. | 5个 |
7.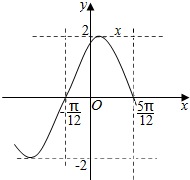 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )| A. | $\sqrt{3}$ | B. | 0 | C. | -2 | D. | 1 |
1.一个直四棱柱的侧棱长等于2,底面是边长为1的正方形,如果其俯视图是一个面积为1的正方形,其侧视图的面积的取值范围是( )
| A. | [1,2] | B. | [2,2$\sqrt{2}$] | C. | [1,2$\sqrt{2}$] | D. | [$\sqrt{3}$,2$\sqrt{2}$] |
8.过点($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),且与圆x2+y2=1相切的直线方程是( )
| A. | y=x+$\sqrt{2}$ | B. | y=-x+$\sqrt{2}$ | C. | y=x-$\sqrt{2}$ | D. | y=-x-$\sqrt{2}$ |