题目内容
3.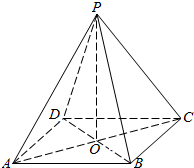 如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:
如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:(1)PA与BC所成角的大小;
(2)PB与底面所成角的大小.
分析 (1)利用平移法求出PA与BC所成角;
(2)确定∠PBO是PB与底面所成角即可.
解答 解:(1)∵AD∥BC,
∴∠PAD(或其补角)是PA与BC所成角,
∵棱锥的侧棱长和底面边长都是2,
∴∠PAD=60°,
∴PA与BC所成角是60°;
(2)∵O为正四棱锥P-ABCD的底面中心,
∴PO⊥平面ABCD,
∴∠PBO是PB与底面所成角,
∵棱锥的侧棱长和底面边长都是2,
∴OB=$\sqrt{2}$,PB=2,
∴∠PBO=45°,
∴PB与底面所成角是45°.
点评 本题考查空间角的计算,考查学生的转化能力,属于中档题.

练习册系列答案
相关题目
14.抛物线x=-4y2的准线方程为( )
| A. | y=1 | B. | y=$\frac{1}{16}$ | C. | x=1 | D. | x=$\frac{1}{16}$ |
8.过点($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),且与圆x2+y2=1相切的直线方程是( )
| A. | y=x+$\sqrt{2}$ | B. | y=-x+$\sqrt{2}$ | C. | y=x-$\sqrt{2}$ | D. | y=-x-$\sqrt{2}$ |
13.已知实数x、y满足不等式组$\left\{\begin{array}{l}{2x-y≤6}\\{x-y-2≥0}\\{x≥a}\end{array}\right.$,若z=3x+y的最小值是8,则实数a=( )
| A. | 2 | B. | -$\frac{2}{7}$ | C. | 14 | D. | $\frac{14}{5}$ |
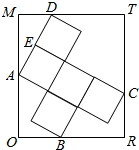 如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.