题目内容
1.两个圆锥有公共底面,且两圆锥的顶点和底面圆周都在同一个球面上.若圆锥底面面积是球面面积的$\frac{3}{16}$,则这两个圆锥的体积之比为( )| A. | 2:1 | B. | 5:2 | C. | 1:4 | D. | 3:1 |
分析 设球半径为r,则根据圆锥底面与球面积的关系得出圆锥的底面半径,根据勾股定理求出球心到圆锥底面的距离,得到两圆锥的高度.
解答 解:设球的半径为R,圆锥底面的半径为r,则πr2=$\frac{3}{16}$×4πR2=$\frac{3π{R}^{2}}{4}$,∴r=$\frac{\sqrt{3}}{2}R$.
∴球心到圆锥底面的距离为$\sqrt{{R}^{2}-{r}^{2}}$=$\frac{R}{2}$.∴圆锥的高分别为$\frac{R}{2}$和$\frac{3R}{2}$.
∴两个圆锥的体积比为$\frac{R}{2}$:$\frac{3R}{2}$=1:3.
故选:D.
点评 本题考查了圆锥的体积计算,球与内接旋转体的关系,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.过直线3x-2y+3=0与x+y-4=0的交点,与直线2x+y-1=0平行的直线方程为( )
| A. | 2x+y-5=0 | B. | 2x-y+1=0 | C. | x+2y-7=0 | D. | x-2y+5=0 |
6.已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有( )
| A. | 2 个 | B. | 3个 | C. | 4个 | D. | 5个 |
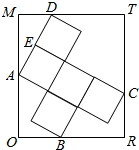 如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.