题目内容
1．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{{3}^{-x}+1，x≤0}\end{array}\right.$，则f（f（1））+f（log3$\frac{1}{2}$）的值是5．分析 利用分段函数的性质求解．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{{3}^{-x}+1，x≤0}\end{array}\right.$，
∴f（1）=log21=0，
f（f（1））=f（0）=3-0+1=2，
f（log3$\frac{1}{2}$）=${3}^{-lo{g}_{3}\frac{1}{2}}$+1=${3}^{lo{g}_{3}2}$+1=2+1=3，
∴f（f（1））+f（log3$\frac{1}{2}$）=2+3=5．
故答案为：5．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
相关题目
16．若向量$\overrightarrow{a}$、$\overrightarrow{b}$，满足|$\overrightarrow{a}$|=1、|$\overrightarrow{b}$|=$\sqrt{2}$，$\overrightarrow{a}$⊥（$\overrightarrow{a}+\overrightarrow{b}$），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{2π}{3}$ | C． | $\frac{3π}{4}$ | D． | $\frac{5π}{6}$ |
13．已知实数x、y满足不等式组$\left\{\begin{array}{l}{2x-y≤6}\\{x-y-2≥0}\\{x≥a}\end{array}\right.$，若z=3x+y的最小值是8，则实数a=（ ）
| A． | 2 | B． | -$\frac{2}{7}$ | C． | 14 | D． | $\frac{14}{5}$ |
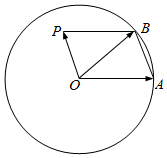已知点A、B为单位圆O上的两点，点P为单位圆0所在平面内的一点，且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线．