题目内容
13.抛物线x=$\frac{1}{4}$y2的焦点坐标为(1,0).分析 根据题意,先将抛物线方程变形为标准方程,分析可得其焦点在x轴上,且p=2,由抛物线焦点坐标公式计算可得答案.
解答 解:抛物线的方程为x=$\frac{1}{4}$y2的,则其标准方程为y2=4x,
其焦点在x轴上,且p=2,
则其焦点坐标为(1,0);
故答案为:(1,0).
点评 本题考查抛物线的几何性质,要先将其方程变形为标准方程.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
3.已知;$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,则f(n+1)-f(n)=( )
| A. | $\frac{1}{2n+1}+\frac{1}{2n+2}$ | B. | $\frac{1}{2n+2}-\frac{1}{n+1}$ | ||
| C. | $\frac{1}{2n+2}$ | D. | $\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$ |
8.已知椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1以及椭圆内一点P(2,1),则以P为中点的弦所在直线斜率为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
5.若复数z满足z(4-i)=5+3i(i为虚数单位),则复数z的共轭复数为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
3.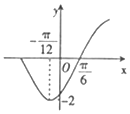 设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
 设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
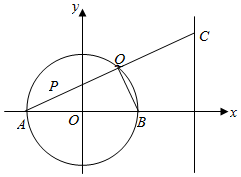 已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.
已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.