题目内容
2.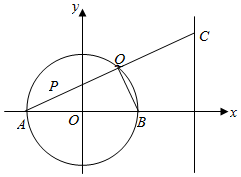 已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.
已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.(1)若过点P的直线l2与圆O相交所得弦长等于4$\sqrt{2}$,求直线l2的方程;
(2)设直线BQ、BC的斜率分别为kBQ、kBC,求证:kBQ•kBC为定值.
分析 (1)若过点P的直线l2与圆O相交所得弦长等于4$\sqrt{2}$,圆心O(0,0)到直线的距离$d=\sqrt{9-{{(2\sqrt{2})}^2}}=1$,分类讨论,求直线l2的方程;
(2)求出相应直线的斜率,即可证明结论.
解答 (1)解:因直线l2与圆O相交所得弦长等于4$\sqrt{2}$,所以圆心O(0,0)到直线的距离$d=\sqrt{9-{{(2\sqrt{2})}^2}}=1$
设直线l2的方程为y-2=k(x+1),即kx-y+k+2=0
由$d=\frac{|k+2|}{{\sqrt{1+{k^2}}}}=1$解得$k=-\frac{3}{4}$
又过点P且与x轴垂直的直线x=-1显然符合要求
所以直线l2的方程是x=-1或3x+4y-5=0---------(6分)
(2)证明:设点C的坐标为(6,h),则直线AC的方程为$y=\frac{h}{9}(x+3)$
由$\left\{\begin{array}{l}y=\frac{h}{9}(x+3)\\{x^2}+{y^2}=9\end{array}\right.⇒\frac{{81+{h^2}}}{h^2}{y^2}-\frac{54}{h}y=0$解得${y_1}=0,{y_2}=\frac{54h}{{81+{h^2}}}$
从而得点$Q(\frac{{243-3{h^2}}}{{81+{h^2}}},\frac{54h}{{81+{h^2}}})$,
所以${k_{BQ}}=-\frac{9}{h},{k_{BC}}=\frac{h}{3}$
所以kBQ•kBC=-3----------(12分)
点评 本题考查直线与圆位置关系的运用,考查斜率的计算,考查学生分析解决问题的能力,属于中档题.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案| A. | $\frac{3}{4}$ | B. | $\frac{8}{9}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{12}$ |
| A. | 增加6.5个单位 | B. | 增加6个单位 | C. | 减少6.5个单位 | D. | 减少6个单 |
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
| A. | 抛物线y=$\frac{1}{4}$x2的焦点坐标为(0,1) | |
| B. | 双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=2的右顶点到其左、右焦点的距离之比为3 | |
| C. | 函数f(x)=x3-3x2+b在区间(-∞,-1)上无极值点 | |
| D. | 曲线f(x)=x3-3x2+5在点(1,f(1))处切线的倾斜角大于$\frac{3π}{4}$ |
| A. | 当且仅当x∈(-∞,1),f(x)<0 | B. | 当且仅当x∈(1,+∞),f(x)>0 | ||
| C. | 对于?x∈R,f(x)<0 | D. | 对于?x∈R,f(x)>0 |