题目内容
3.已知;$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,则f(n+1)-f(n)=( )| A. | $\frac{1}{2n+1}+\frac{1}{2n+2}$ | B. | $\frac{1}{2n+2}-\frac{1}{n+1}$ | ||
| C. | $\frac{1}{2n+2}$ | D. | $\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$ |
分析 利用$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,计算f(n+1)-f(n)即可.
解答 解:∵$f(n)=\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}$,
∴f(n+1)-f(n)=$\frac{1}{2n+1}+\frac{1}{2n+2}-\frac{1}{n+1}$,
故选:D.
点评 本题考查归纳推理,考查学生的计算能力,正确计算是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在△ABC中,已知三个内角为A,B,C满足sinA:sinB:sinC=6:5:4,则sinB=( )
| A. | $\frac{{\sqrt{7}}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{{5\sqrt{7}}}{16}$ | D. | $\frac{9}{16}$ |
11.已知x1,x2是方程(x-1)2=-3的两个相异根,当x1=1-$\sqrt{3}$i(i为虚数单位)时,则x22为( )
| A. | 4+2$\sqrt{3}$i | B. | -2+2$\sqrt{3}$i | C. | 4-2$\sqrt{3}$i | D. | -2-2$\sqrt{3}$i |
8.已知a=log2$\frac{1}{8}$,b=0.33.2,c=3.20.3,则实数a,b,c的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
15.以下说法错误的是( )
| A. | 推理一般分为合情推理和演绎推理 | |
| B. | 归纳是从特殊到一般的过程,它属于合情推理 | |
| C. | 在数学中,证明命题的正确性既能用演绎推理又能用合情推理 | |
| D. | 演绎推理经常使用的是由大前提、小前提得到结论的三段论推理 |
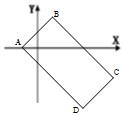 如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.
如图,已知复平面内平行四边形ABCD中,点A对应的复数为-1,$\overrightarrow{AB}$对应的复数为2+2i,$\overrightarrow{BC}$对应的复数为4-4i.