题目内容
1.已知函数f(x)=$\frac{1}{3}{x^3}-{x^2}+({1-{m^2}})x({0<m<1})$(1)求函数f(x)的极大值点和极小值点;
(2)若f(x)恰好有三个零点,求实数m取值范围.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值点;
(2)问题转化为关于m的不等式组,解出即可.
解答 解:(1)令f'(x)=x2-2x+1-m2=0,得x1=1-m;x2=1+m,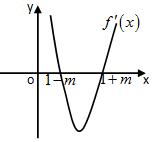 ,
,
x,f′(x),f(x)的变化如下:
| x | (-∞,1-m) | (1-m,1+m) | (1+m,+∞) |
| f'(x) | + | - | + |
| f(x) | 递增 | 递减 | 递增 |
函数f(x)的极大值点为x=1-m,极小值点为x=1+m;
(2)若f(x)恰好有三个零点,
则$\left\{{\begin{array}{l}{f({1-m})>0}\\{f({1+m})<0}\end{array}}\right.$,又0<m<1,得:$\frac{1}{2}<m<1$.
点评 本题考查了函数的单调性、极值点问题,考查导数的应用以及函数的零点问题,是一道中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
11.已知x1,x2是方程(x-1)2=-3的两个相异根,当x1=1-$\sqrt{3}$i(i为虚数单位)时,则x22为( )
| A. | 4+2$\sqrt{3}$i | B. | -2+2$\sqrt{3}$i | C. | 4-2$\sqrt{3}$i | D. | -2-2$\sqrt{3}$i |
9.已知函数f(x)在R上可导,且f(x)=2x+f'(0)•(x2-1),则f(0)的值为( )
| A. | ln2 | B. | 0 | C. | 1 | D. | 1-ln2 |
6.已知向量$\overrightarrow{m}$,$\overrightarrow{n}$分别是直线l和平面α的方向向量和法向量,若$\overrightarrow{m}$与$\overrightarrow{n}$夹角的余弦等于$\frac{1}{2}$,则l与α所成的角为( )
| A. | 60° | B. | 30° | C. | 120° | D. | 150° |
10.甲、乙两人约定在下午 4:30:5:00 间在某地相见,且他们在 4:30:5:00 之间 到达的时刻是等可能的,约好当其中一人先到后一定要等另一人 20 分钟,若另一人仍不到则可以离去,则这两人能相见的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{8}{9}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{12}$ |
11.已知命题p:?x∈R,3x-3≤0.若(¬p)∧q是假命题,则命题q可以是( )
| A. | 抛物线y=$\frac{1}{4}$x2的焦点坐标为(0,1) | |
| B. | 双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=2的右顶点到其左、右焦点的距离之比为3 | |
| C. | 函数f(x)=x3-3x2+b在区间(-∞,-1)上无极值点 | |
| D. | 曲线f(x)=x3-3x2+5在点(1,f(1))处切线的倾斜角大于$\frac{3π}{4}$ |