题目内容
18.已知中心在原点,焦点在x轴上的椭圆的一个顶点坐标为(0,1),其离心率为$\frac{\sqrt{6}}{3}$(1)求椭圆的标准方程;
(2)椭圆上一点P满足∠F1PF2=60°,其中F1,F2为椭圆的左右焦点,求△F1PF2的面积.
分析 (1)设椭圆的方程,则b=1,根据椭圆的离心率即可求得a的值,即可求得椭圆方程;
(2)根据余弦定理,即可求得丨PF1丨•丨PF1丨,利用三角形的面积公式即可求得△F1PF2的面积.
解答 解:(1)设椭圆的标准方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
椭圆的一个顶点为(0,1)则b=1,…(2分)
由椭圆的离心率e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{6}}{3}$,解得:a2=3,…(4分)
椭圆的标准方程为$\frac{{x}^{2}}{3}+{y}^{2}=1$; …(6分)
(2)设丨PF1丨=n,丨PF2丨=m,∠F1PF2=60°,
由余弦定理可知:丨F1F2丨2=丨PF1丨2+丨PF2丨2-2丨PF1丨•丨PF1丨cos60°,
4c2=m2+n2-2mncos60°=(m+n)2-3mn=4a2-3mn,
则4×($\sqrt{2}$)2=4a2-3mn,解得:mn=$\frac{4}{3}$,
即丨PF1丨•丨PF1丨=$\frac{4}{3}$,…(8分)
△F1PF2的面积S=$\frac{1}{2}$×丨PF1丨丨PF1丨×sin∠F1PF2,
∴${S_{△{F_1}P{F_2}}}=\frac{1}{2}×\frac{4}{3}×\frac{{\sqrt{3}}}{2}=\frac{{\sqrt{3}}}{3}$,
△F1PF2的面积$\frac{\sqrt{3}}{3}$.…(12分)
点评 本题考查椭圆的标准方程,考查余弦定理,三角形的面积公式,考查计算能力,属于中档题.

| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |
| A. | ln2 | B. | 0 | C. | 1 | D. | 1-ln2 |
| A. | 60° | B. | 30° | C. | 120° | D. | 150° |
| A. | $-\frac{{\sqrt{35}}}{18}$ | B. | $\frac{{\sqrt{35}}}{18}$ | C. | $\frac{17}{18}$ | D. | $-\frac{17}{18}$ |
| A. | $\frac{3}{4}$ | B. | $\frac{8}{9}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{12}$ |
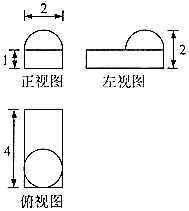
| A. | 8+$\frac{4}{3}$π | B. | 8+$\frac{2}{3}$π | C. | 4+$\frac{4π}{3}$ | D. | 4+$\frac{2π}{3}$ |