题目内容
3.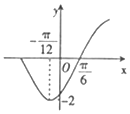 设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )
设函数f(x)=cos2x-$\sqrt{3}$sin2x,把y=f(x)的图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后,得到的部分图象如图所示,则f(φ)的值等于( )| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律得到平移后的函数解析式,再根据平移后的图象知,平移后的图象在$x=-\frac{π}{12}$处取最小值,由此求得φ的值,可得f(φ)的值.
解答 解:函数$f(x)=cos2x-\sqrt{3}sin2x=2cos({2x+\frac{π}{3}})$,然后将其图象向左平移$φ({|φ|<\frac{π}{2}})$个单位后得到$y=2cos[{2({x+φ})+\frac{π}{3}}]=2cos({2x+2φ+\frac{π}{3}})$,
由平移后的图象知,平移后的图象在$x=-\frac{π}{12}$处取最小值,则$2×({-\frac{π}{12}})+2φ+\frac{π}{3}=2kπ+π,k∈Z$,∴$φ=kπ+\frac{5}{12}π,k∈Z$.
又$|φ|<\frac{π}{2}$,∴$φ=\frac{5π}{12}$,$f(φ)=2cos({2×\frac{5}{12}π+\frac{π}{3}})=2cos\frac{7}{6}π=-\sqrt{3}$,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,五点法作图,属于基础题.

练习册系列答案
相关题目
14.已知A,B分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,不同两点P,Q在双曲线C上,且关于x轴对称,设直线AP,BQ的斜率分别为λ,μ,则当$\frac{16}{λμ}$+λμ取最大值时,双曲线C的离心率为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
11.已知命题p:?x∈R,3x-3≤0.若(¬p)∧q是假命题,则命题q可以是( )
| A. | 抛物线y=$\frac{1}{4}$x2的焦点坐标为(0,1) | |
| B. | 双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=2的右顶点到其左、右焦点的距离之比为3 | |
| C. | 函数f(x)=x3-3x2+b在区间(-∞,-1)上无极值点 | |
| D. | 曲线f(x)=x3-3x2+5在点(1,f(1))处切线的倾斜角大于$\frac{3π}{4}$ |
8.某几何体的三视图如图所示,则该几何体的体积是( )
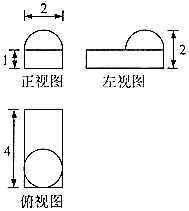

| A. | 8+$\frac{4}{3}$π | B. | 8+$\frac{2}{3}$π | C. | 4+$\frac{4π}{3}$ | D. | 4+$\frac{2π}{3}$ |
15.已知$\overrightarrow{a}$=(3,2),$\overrightarrow{b}$=(6,y),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则y等于( )
| A. | -9 | B. | -4 | C. | 4 | D. | 9 |
12.定义R上的减函数f(x),其导函数f'(x)满足$\frac{f(x)}{f'(x)}<1-x$,则下列结论正确的是( )
| A. | 当且仅当x∈(-∞,1),f(x)<0 | B. | 当且仅当x∈(1,+∞),f(x)>0 | ||
| C. | 对于?x∈R,f(x)<0 | D. | 对于?x∈R,f(x)>0 |
7.某几何体的三视图如图所示,则其体积为( )


| A. | 80 | B. | 160 | C. | 240 | D. | 480 |