题目内容
已知(a,b)是关于x的一元二次不等式mx2-2x+1<0的解集,则2a+b的最小值为( )
A、3+2
| ||||
B、
| ||||
C、5+2
| ||||
D、
|
考点:一元二次不等式的解法
专题:导数的概念及应用,不等式的解法及应用
分析:根据题意,求出m的取值范围以及a、b的值,得出2a+b的表达式;
再构造函数,求出2a+b的最小值即可.
再构造函数,求出2a+b的最小值即可.
解答:
解:∵(a,b)是不等式mx2-2x+1<0的解集,
∴a,b是方程mx2-2x+1=0的两个实数根,
∴
;
解得0<m<1,
解方程得a=
,b=
;
∴2a+b=
=
-
;
设
=t(t>1),
∴f(t)=3t-
;
∴f′(t)=3-
•
•(2t-1)=3-
,
令f′(t)=0,
解得t=
,或t=
(不合题意,舍去);
∴当t=
时,f(t)取得最小值
,
∴2a+b的最小值为
.
故选:B.
∴a,b是方程mx2-2x+1=0的两个实数根,
∴
|
解得0<m<1,
解方程得a=
1-
| ||
| m |
1+
| ||
| m |
∴2a+b=
3-
| ||
| m |
| 3 |
| m |
(
|
设
| 1 |
| m |
∴f(t)=3t-
| t2-t |
∴f′(t)=3-
| 1 |
| 2 |
| 1 | ||
|
| 2t-1 | ||
2
|
令f′(t)=0,
解得t=
4+3
| ||
| 8 |
4-3
| ||
| 8 |
∴当t=
4+3
| ||
| 8 |
3+2
| ||
| 2 |
∴2a+b的最小值为
3+2
| ||
| 2 |
故选:B.
点评:本题考查了导数的概念与应用的问题,也考查了不等式的解法与应用的问题,考查了构造函数的思想方法,是综合性题目.

练习册系列答案
相关题目
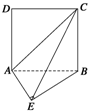 如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )
如图所示,在直二面角D-AB-E中,四边形ABCD是边长为2的正方形,△AEB是等腰直角三角形,其中∠AEB=90°,则点D到平面ACE的距离为( )