题目内容
正方体ABCD-A1B1C1D1的棱长为2,E为棱A1B1中点,P、Q分别为棱AD,DC上的动点,则四面体PEA1Q体积的最大值为 .
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:根据图形得出S △A1EQ=
×1×2
=
,判断出当P到面A1EQ的距离最大时,在A与P重合,求出距离的最大值,运用体积公式即可.
| 1 |
| 2 |
| 2 |
| 2 |
解答:
解:∵正方体ABCD-A1B1C1D1的棱长为2,E为棱A1B1中点,P、Q分别为棱AD,DC上的动点,Q到直线A1E的距离为定值2
,
∴S △A1EQ=
×1×2
=
,
∴
即d=
AD1=
×2
=
,
∴四面体PEA1Q体积的最大值为
×
×
=

故答案为:
| 2 |
∴S △A1EQ=
| 1 |
| 2 |
| 2 |
| 2 |
∴
即d=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴四面体PEA1Q体积的最大值为
| 1 |
| 3 |
| 2 |
| 2 |
| 2 |
| 3 |

故答案为:
| 2 |
| 3 |
点评:本题考查了空间几何题的性质,求解体积最大值的问题转化为面积,距离的最值问题,属于中档题,有一定的难度.

练习册系列答案
相关题目
两条异面直线AB、CD分别在两平行平面α、β上,α、β间的距离为d,若三棱锥A-BCD为正四面体,则其体积为( )
A、
| ||
B、
| ||
| C、d3 | ||
D、
|
已知(a,b)是关于x的一元二次不等式mx2-2x+1<0的解集,则2a+b的最小值为( )
A、3+2
| ||||
B、
| ||||
C、5+2
| ||||
D、
|
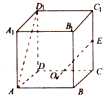 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于