题目内容
已知椭圆
+
=1,F2是其右焦点,F1为左焦点也是抛物线y2=-4x的焦点,过F1的直线L与椭圆交于A、B两点,与抛物线交于C、D两点,当直线L与x轴垂直时
=2
.
(1)求椭圆的方程;
(2)求
•
的最大值和最小值.
| x2 |
| a2 |
| y2 |
| b2 |
| |CD| |
| |AB| |
| 2 |
(1)求椭圆的方程;
(2)求
| F1A |
| F2B |
考点:直线与圆锥曲线的关系,椭圆的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(1)由抛物线方程和题意求椭圆中c的值,根据椭圆与抛物线的通径比列出a,b关系式,求出a、b的值即可;
(2)设A、B的坐标和直线l方程,并对直线l的斜率进行分类讨论,直线l方程与椭圆方程联立消去y,由韦达定理得x1x2与x1+x2,代入
•
化简得到关于k的式子,利用分离常数法、函数的性质求出其范围,即可
•
的范围,进而求出最值.
(2)设A、B的坐标和直线l方程,并对直线l的斜率进行分类讨论,直线l方程与椭圆方程联立消去y,由韦达定理得x1x2与x1+x2,代入
| F2A |
| F2B |
| F2A |
| F2B |
解答:
解:(1)由抛物线y2=-4x的焦点是(-1,0),得椭圆的左焦点F1为(-1,0),即c=1,
因为过F1的直线l与x轴垂直,所以AB为椭圆通径,CD为抛物线通径,
则|AB|=
,|CD|=2p=4,所以
=
=2
,即b2=
a,
因为a2=b2+c2,得a=
,b=1,所以椭圆方程为
+y2=1,
(2)设A(x1,y1),B(x2,y2)
①当直线l斜率存在时,设方程为y=k(x+1),
由
得,(2k2+1)x2+4k2x+2(k2-1)=0,
则△=(4k2)2-4(2k2+1)×2(k2-1)=8k2+8>0,
x1+x2=-
,x1x2=
,
所以
•
=(x1-1)(x2-1)+y1y2=x1x2-(x1+x2)+1+k2(x1+1)(x2+1)
=(1+k2)x1x2+(k2-1)(x1+x2)+1+k2
=(1+k2)×
+(k2-1)×(-
)+1+k2
=
=
=
-
,
因为k2≥0,所以-1≤
-
<
,
所以
•
∈[-1,
),
②当直线l斜率不存在时,可得A(-1,
)B(-1,-
),此时
•
=
,
综上得,
•
∈[-1,
],
所以
•
的最大值和最小值分别为
、-1.
因为过F1的直线l与x轴垂直,所以AB为椭圆通径,CD为抛物线通径,
则|AB|=
| 2b2 |
| a |
| |CD| |
| |AB| |
| 4 | ||
|
| 2 |
| ||
| 2 |
因为a2=b2+c2,得a=
| 2 |
| x2 |
| 2 |
(2)设A(x1,y1),B(x2,y2)
①当直线l斜率存在时,设方程为y=k(x+1),
由
|
则△=(4k2)2-4(2k2+1)×2(k2-1)=8k2+8>0,
x1+x2=-
| 4k2 |
| 2k2+1 |
| 2(k2-1) |
| 2k2+1 |
所以
| F2A |
| F2B |
=(1+k2)x1x2+(k2-1)(x1+x2)+1+k2
=(1+k2)×
| 2(k2-1) |
| 2k2+1 |
| 4k2 |
| 2k2+1 |
=
| 7k2-1 |
| 2k2+1 |
| ||||
| 2k2+1 |
| 7 |
| 2 |
| 9 |
| 2(2k2+1) |
因为k2≥0,所以-1≤
| 7 |
| 2 |
| 9 |
| 2(2k2+1) |
| 7 |
| 2 |
所以
| F2A |
| F2B |
| 7 |
| 2 |
②当直线l斜率不存在时,可得A(-1,
| ||
| 2 |
| ||
| 2 |
| F2A |
| F2B |
| 7 |
| 2 |
综上得,
| F2A |
| F2B |
| 7 |
| 2 |
所以
| F2A |
| F2B |
| 7 |
| 2 |
点评:本题考查椭圆、抛物线的标准方程,向量、直线与圆锥曲线的综合应用,以及对直线的斜率进行讨论,这是易忘的地方,考查利用韦达定理达到设而不求思想和计算化简能力.

练习册系列答案
相关题目
已知a>0,b>0,若直线l:ax+by=1平分圆x2+y2-2x-2y-3=0的周长,则
+
的最小值为( )
| 1 |
| a |
| 2 |
| b |
A、4
| ||
B、3+2
| ||
C、2
| ||
| D、1 |
两条异面直线AB、CD分别在两平行平面α、β上,α、β间的距离为d,若三棱锥A-BCD为正四面体,则其体积为( )
A、
| ||
B、
| ||
| C、d3 | ||
D、
|
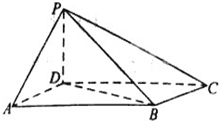 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,且∠DAB=60°,AB=2AD=2,PD⊥底面ABC,则:
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,且∠DAB=60°,AB=2AD=2,PD⊥底面ABC,则:(1)证明:PA⊥BD;
(2)若PD=AD,求平面APB与平面CPB夹角的余弦值.
已知(a,b)是关于x的一元二次不等式mx2-2x+1<0的解集,则2a+b的最小值为( )
A、3+2
| ||||
B、
| ||||
C、5+2
| ||||
D、
|
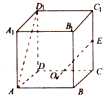 如图,在棱长为2的正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于
如图,在棱长为2的正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,E为CC1的中点,那么异面直线OE与AD1所成角的余弦值等于