题目内容
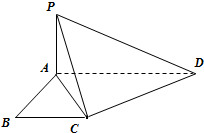 如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.
如图,已知ABCD是直角梯形,∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面BCME.(1)若E是PA的中点,证明:BE∥平面PCD;
(2)若PA=3,求三棱锥B-PCD的体积;
(3)证明:PC⊥CD.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间向量及应用
分析:(1)(方法一)取AD的中点为F,连结BF,EF.利用中位线性质,确定平行线,再运用线面平行的判断定定理即可证明.
(方法二):取PD的中点为M,连结EM,CM.利用中位线,得出平行线,判断出;四边形BCME是平行四边形,即可证明.
(2)所抓化为VB-PCD=VP-BCD=
×PA×S△BCD=
×3×
=
.
(3)PA⊥CD.PA∩AC=A,CD⊥平面PAC,得出CD⊥平面PAC,得证CD⊥PC.
(方法二):取PD的中点为M,连结EM,CM.利用中位线,得出平行线,判断出;四边形BCME是平行四边形,即可证明.
(2)所抓化为VB-PCD=VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)PA⊥CD.PA∩AC=A,CD⊥平面PAC,得出CD⊥平面PAC,得证CD⊥PC.
解答:
证明:法一:(1)取AD的中点为F,连结BF,EF.
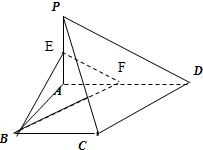
∵AD=2,BC=1,
∴BC∥FD,且BC=FD,
∴四边形BCDE是平行四边形,
即BF∥CD.
∵BF?平面PCD,
∴BF∥平面PCD
∵E,F分别是PA,AD的中点∴EF∥PD
∵EF?平面PCD,
∴EF∥平面PCD.
∵EF∩BF=F,
∴平面BEF∥平面PCD.
∵BE?平面BEF,
∴BE∥平面PCD.
法二:取PD的中点为M,连结EM,CM.
∵E为PA的中点,∴EM∥
AD,BC∥
AD,∴EM∥
BC且EM=BC
∴四边形BCME是平行四边形
即BE∥CM,
∵BE?平面PCD,
CM?平面PCD
∴BE∥平面PCD.
(2)由已知得S△BCD=
×1×1=
,
所以 VB-PCD=VP-BCD=
×PA×S△BCD=
×3×
=
.
(3)证明:由已知易得AC=
,CD=
.
∵AC2+CD2=AD2
∴∠ACD=90°,即AC⊥CD.
又∵PA⊥平面ABCD,CD?平面ABCD
∴PA⊥CD.
∵PA∩AC=A,
∴CD⊥平面PAC.
∵PC?平面PAC,
∴CD⊥PC.

∵AD=2,BC=1,
∴BC∥FD,且BC=FD,
∴四边形BCDE是平行四边形,
即BF∥CD.
∵BF?平面PCD,
∴BF∥平面PCD
∵E,F分别是PA,AD的中点∴EF∥PD
∵EF?平面PCD,
∴EF∥平面PCD.
∵EF∩BF=F,
∴平面BEF∥平面PCD.
∵BE?平面BEF,
∴BE∥平面PCD.
法二:取PD的中点为M,连结EM,CM.
∵E为PA的中点,∴EM∥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形BCME是平行四边形
即BE∥CM,
∵BE?平面PCD,
CM?平面PCD
∴BE∥平面PCD.
(2)由已知得S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
所以 VB-PCD=VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)证明:由已知易得AC=
| 2 |
| 2 |
∵AC2+CD2=AD2
∴∠ACD=90°,即AC⊥CD.
又∵PA⊥平面ABCD,CD?平面ABCD
∴PA⊥CD.
∵PA∩AC=A,
∴CD⊥平面PAC.
∵PC?平面PAC,
∴CD⊥PC.
点评:本题综合考查了空间几何体的性质,运用证明平行,垂直,求解体积问题,属于综合题,难度较大.

练习册系列答案
相关题目
数列{an}满足:a1=1,a2=2,an=
(n≥3且n∈N),则a2014=( )
| an-1 |
| an-2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2-2014 |
已知数列{an}满足an=
(k∈N*),设f(n)=a1+a2+a3+…+a2n-1+a2n,则f(2014)-f(2013)=( )
|
| A、42012 |
| B、42013 |
| C、42014 |
| D、42015 |
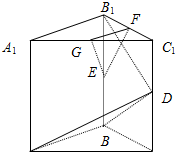 在直三棱柱ABCA1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证:
在直三棱柱ABCA1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证: