题目内容
数列{an}满足a1+3a2+32a3+…+3n-1an=
,则数列{an}的通项公式为 .
| n |
| 3 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:构造新数列,利用作差法即可.
解答:
解:当n≥2时,a1+3a2+32a3+…+3n-1an=
,
a1+3a2+32a3+…+3n-2an-1=
,
两式相减得3n-1an=
-
=
,
则an=
,
当n=1时,a1=
满足an=
,
综上an=
.
故答案为:an=
| n |
| 3 |
a1+3a2+32a3+…+3n-2an-1=
| n-1 |
| 3 |
两式相减得3n-1an=
| n |
| 3 |
| n-1 |
| 3 |
| 1 |
| 3 |
则an=
| 1 |
| 3n |
当n=1时,a1=
| 1 |
| 3 |
| 1 |
| 3n |
综上an=
| 1 |
| 3n |
故答案为:an=
| 1 |
| 3n |
点评:本题主要考查数列通项公式的求解,根据作差法是解决本题的关键.

练习册系列答案
相关题目
数列{an}满足:a1=1,a2=2,an=
(n≥3且n∈N),则a2014=( )
| an-1 |
| an-2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2-2014 |
已知数列{an}满足an=
(k∈N*),设f(n)=a1+a2+a3+…+a2n-1+a2n,则f(2014)-f(2013)=( )
|
| A、42012 |
| B、42013 |
| C、42014 |
| D、42015 |
若圆C1:x2+y2-2x=0与直线l:y-mx-m=0有两个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
若点P(-1,-1)在圆x2+y2+4mx-2y+5m=0的外部,则实数m的取值范围为( )
| A、(-4,+∞) | ||
B、(-∞,
| ||
C、(-4,
| ||
D、(
|
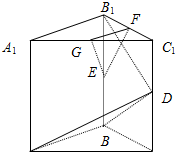 在直三棱柱ABCA1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证:
在直三棱柱ABCA1B1C1中,∠ABC=90°,BC=2,CC1=4,点E在线段BB1上,且EB1=1,D,F,G分别为CC1,C1B1,C1A1的中点.求证: