题目内容
直线l:y=x-1与抛物线C:y2=2px(p>0)相交于A,B两点,且l过C的焦点.
(1)求抛物线C的方程;
(2)若以AB为直径作圆Q,求圆Q的方程.
(1)求抛物线C的方程;
(2)若以AB为直径作圆Q,求圆Q的方程.
考点:双曲线的简单性质,圆的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)求出C的焦点,可得抛物线C的方程;
(2)直线l:y=x-1与抛物线联立,求出|AB|,Q的坐标,即可求圆Q的方程.
(2)直线l:y=x-1与抛物线联立,求出|AB|,Q的坐标,即可求圆Q的方程.
解答:
解:(1)直线l:y=x-1,令y=0可得x=1,
∴C的焦点(1,0),
∴抛物线C的方程y2=4x; …(6分)
(2)设A(x1,y1),B(x2,y2).
直线l:y=x-1与抛物线联立可得x2-6x+1=0,…(9分)
由抛物线的定义可知,|AB|=x1+x2+p=8,
AB的中点坐标为(3,2),
∴圆Q的方程为(x-3)2+(y-2)2=16 …(13分)
∴C的焦点(1,0),
∴抛物线C的方程y2=4x; …(6分)
(2)设A(x1,y1),B(x2,y2).
直线l:y=x-1与抛物线联立可得x2-6x+1=0,…(9分)
由抛物线的定义可知,|AB|=x1+x2+p=8,
AB的中点坐标为(3,2),
∴圆Q的方程为(x-3)2+(y-2)2=16 …(13分)
点评:本题主要考查圆的方程,考查了抛物线的标准方程,以及过焦点的直线与抛物线相交的弦长等问题,属于中档题.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=3,DE=4.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=3,DE=4.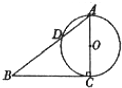 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,求 BD的长.
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,求 BD的长.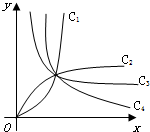 如图的曲线是幂函数y=xn在第一象限内的图象,已知n分别取a,b,c,d四个值,与曲线C1,C2,C3,C4相应,则a,b,c,d四个值从小到大依次为
如图的曲线是幂函数y=xn在第一象限内的图象,已知n分别取a,b,c,d四个值,与曲线C1,C2,C3,C4相应,则a,b,c,d四个值从小到大依次为