题目内容

解下列不等式．
（1）2x2-3x-2＞0；
（2）-2x2+3x-5≥0．
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：（1）2x2-3x-2＞0化为（2x+1）（x-2）＞0，利用一元二次不等式的解法即可得出；
（2）-2x2+3x-5≥0化为2x2-3x+5≤0，由于△＜0，即可得出不等式的解集．
解答： 解：（1）2x2-3x-2＞0化为（2x+1）（x-2）＞0，解得x＞2或x＜-
1
2
，其解集为{x|x＞2或x＜-
1
2
}；
（2）-2x2+3x-5≥0化为2x2-3x+5≤0，∵△=9-40＜0，∴不等式的解集为∅．
点评：本题考查了一元二次不等式的解法、解集与判别式的关系，属于基础题．
练习册系列答案
相关题目
设i是虚数单位，复数z=
1+ki
2-i
．
（Ⅰ）若z=
1
2
，求实数k的值；      
（Ⅱ）若z为纯虚数，求复数z．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4（
2
+1）．一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任一点．
（1）求椭圆和双曲线的标准方程；
（2）设直线PF1、PF2的斜率分别为k1、k2，证明：k1•k2=1．
已知函数f（x）=log2（2x+1）-kx为偶函数．
（1）求实数k的值；
（2）求证：f（x）在（0，+∞）上为增函数；
（3）若?t∈R，都有f（t2+2t+3）＞f（m），求实数m的取值范围．
若f（x）=
3
cos2ax-sinaxcosax（a＞0）的图象与直线y=m（m＞0）相切，并且切点横坐标依次成公差为π的等差数列．
（1）求a和m的值；
（2）△ABC中a、b、c分别是∠A、∠B、∠C的对边．若（
A
2
，
3
2
）是函数f（x）图象的一个对称中心，且a=4，求△ABC面积的最大值．
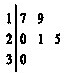某车间共有12名工人，随机抽取6名，他们某日加工零件个数的茎叶图如图所示，其中茎为十位数，叶为个位数．
（1）若日加工零件个数大于样本均值的工人为优秀工人，根据茎叶图推断该车间12名工人中有几名优秀工人？
（2）从这6名工人中任取2人，设这两人加工零件的个数分别为x、y，求|x-y|≤2的概率．
等比数列an中的前三项a1，a2，a3分别是下面数阵中第一、二、三行中的某三个数，且三个数不在同一列．
543
6108
20126

（1）求此数列{an}的通项公式；
（2）若数列{bn}满足bn=3an-（-1）nlgan，求数列{bn}的前n项和Sn．
定长为3的线段AB的两个端点A、B分别在x轴、y轴上滑动，动点P满足
BP
=2
PA
．
（Ⅰ）求点P的轨迹曲线C的方程；
（Ⅱ）若过点（1，0）的直线与曲线C交于M、N两点，求
OM
•
ON
的最大值．
抛物线x=ay2（a＞0）的交点坐标是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网