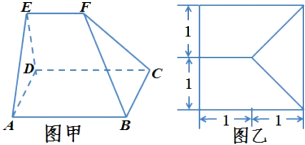
题目内容

9．若复数z满足：i•z=$\sqrt{3}$+i（i是虚数单位），则|z|=2．

分析 求出z，根据复数求模公式求出z的模即可．

解答 解：由iz=$\sqrt{3}$+i，得z=$\frac{\sqrt{3}+i}{i}$=1-$\sqrt{3}$i，
故|z|=$\sqrt{1+3}$=2，
故答案为：2．

点评 本题考查了复数求模公式，复数的化简，是一道基础题．

练习册系列答案
相关题目
19．已知M={x||5-2x|-1＜2}，N={x|x2-5x+6＜0}
求：（1）M∪N；
（2）M∩（∁RN）．
20．已知函数$f（x）=\left\{\begin{array}{l}{log_2}（{-x}），x＜0\\ x-2，x≥0\end{array}\right.$，若函数g（x）=|f（x）|-a有四个不同零点x1，x2，x3，x4，且x1＜x2＜x3＜x4，则${x_1}{x_2}{a^2}-\frac{{{x_3}+{x_4}}}{2}a+2017$的最小值为2016．
17．平面直角坐标系中，给出点A（1，0），B（4，0），若直线x+my-1=0存在点P，使得|PA|=2|PB|，则实数m的取值范围是m≥$\sqrt{3}$或m≤-$\sqrt{3}$．
4．若a＜b＜0，则下列不等式关系中，不能成立的是（　　）
A．$\frac{1}{a}$$＞\frac{1}{b}$B．$\frac{1}{a-b}$$＞\frac{1}{a}$C．a${\;}^{\frac{1}{3}}$$＜{b}^{\frac{1}{3}}$D．a2＞b2
14．定义在R上的偶函数y=f（x），当x≥0时，f（x）=lg（x2-3x+3），则f（x）在R上的零点个数为4个．
1．奇函数f（x）在区间[3，6]上是增函数，在区间[3，6]上的最大值为8，最小值为-1，则f（6）+f（-3）的值为（　　）
A．10B．-10C．9D．15
18．多面体ABCDEF（如图甲）的俯视图如图乙，己知面ADE为正三角形．
（1）求多面体ABCDEF的体积；
（2）求二面角A-BF-C的余弦值．
19．直线l：y=kx+m与椭圆C：$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1．
（1）原点到l的距离为1，求出k和m的关系；
（2）若l与C交于A，B两点，且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0，求出k和m的关系．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网