题目内容
19.直线l:y=kx+m与椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1.(1)原点到l的距离为1,求出k和m的关系;
(2)若l与C交于A,B两点,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,求出k和m的关系.
分析 (1)利用点到直线的距离公式即可得出.
(2)设A(x1,y1),B(x2,y2),直线方程与椭圆方程联立化为:(3+4k2)x2+8kmx+4m2-12=0,△>0,化为:4k2+3>m2.由$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,可得x1x2+y1y2=0,即x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=0,代入即可得出.
解答 解:(1)由题意可得:$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,可得m2=1+k2.
(2)设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,化为:(3+4k2)x2+8kmx+4m2-12=0,
△=64k2m2-4(3+4k2)(4m2-12)>0,化为:4k2+3>m2.
∴x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,x1+x2=$\frac{-8km}{3+4{k}^{2}}$,
∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
∴x1x2+y1y2=0,
∴x1x2+(kx1+m)(kx2+m)=(1+k2)x1x2+km(x1+x2)+m2=0,
∴(1+k2)×$\frac{4{m}^{2}-12}{3+4{k}^{2}}$+km•$\frac{-8km}{3+4{k}^{2}}$+m2=0,
化为:7m2-12k2=12(4k2+3>m2).
点评 本题考查了椭圆的标准方程及其性质、数量积运算性质、一元二次方程的根与系数的关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | x2=2y | B. | x2=4y | C. | x2=8y | D. | x2=16y |
| A. | 10 | B. | 35 | C. | 32 | D. | 25 |
| A. | 2 | B. | 4 | C. | 12 | D. | 24 |
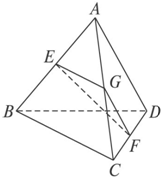 如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.
如图,点A是BCD所在平面外一点,AD=BC,E、F分别是 AB、CD的中点,且EF=$\frac{{\sqrt{2}}}{2}$AD,求异面直线AD和BC所成的角.