题目内容
17.平面直角坐标系中,给出点A(1,0),B(4,0),若直线x+my-1=0存在点P,使得|PA|=2|PB|,则实数m的取值范围是m≥$\sqrt{3}$或m≤-$\sqrt{3}$.分析 根据题意,设出点P(1-my,y),代入|PA|=2|PB|,化简得(4-m2)y2-8y+16=0,由△≥0,求出实数m的取值范围.
解答 解:设P(1-my,y),
∵|PA|=2|PB|,
∴|PA|2=4|PB|2,
∴(1-my-1)2+y2=4(1-my-4)2+y2,
化简得(m2+1)y2+8my+12=0
则△=64m2-48m2-48≥0,
解得m≥$\sqrt{3}$或m≤-$\sqrt{3}$,
即实数m的取值范围是m≥$\sqrt{3}$或m≤-$\sqrt{3}$.
故答案为:m≥$\sqrt{3}$或m≤-$\sqrt{3}$.
点评 本题考查了直线方程的应用问题,也考查了两点间的距离公式的应用问题,是基础题目.

练习册系列答案
相关题目
8.椭圆上$\frac{x^2}{25}+\frac{y^2}{9}=1$上一点p到两焦点距离之积为m,则m取最大值时,p点的坐标是( )
| A. | $({\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$或 $({-\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$ | B. | $({\frac{5}{2},\frac{{3\sqrt{3}}}{2}})$或$({\frac{5}{2},-\frac{{3\sqrt{3}}}{2}})$ | ||
| C. | (5,0)或(-5,0) | D. | (0,3)或(0,-3) |
7.已知抛物线C:x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与C的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$,则抛物线C的方程为( )
| A. | x2=2y | B. | x2=4y | C. | x2=8y | D. | x2=16y |
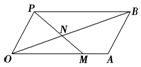 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.