题目内容
19.已知M={x||5-2x|-1<2},N={x|x2-5x+6<0}求:(1)M∪N;
(2)M∩(∁RN).
分析 先化简M,N,再根据并集和补集和交集的定义即可求出.
解答 解:(1)由|5-2x|-1<2,即|5-2x|<3,即-3<5-2x<3,解得1<x<4,即M=(1,4),
N={x|x2-5x+6<0}=(2,3),
∴M∪N=(1,4)
(2)∁RN=(-∞,2]∪[3,+∞)
∴M∩(∁RN)=(1,2]∪[3,4)
点评 此题考查了交、并、补集的混合运算,熟练掌握交、并、补集的定义是解本题的关键.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
9.若等差数列{an}中,a3=3,则{an}的前5项和S5等于( )
| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
4.下列函数中,是偶函数且不存在零点的是( )
| A. | y=x2 | B. | y=$\sqrt{x}$ | C. | y=log2x | D. | y=($\frac{1}{2}$)|x| |
11.设a、b分别是甲、乙各抛掷一枚骰子得到的点数,已知乙所得的点数为2,则方程x2+ax+b=0有两个不相等的实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{12}$ |
8.椭圆上$\frac{x^2}{25}+\frac{y^2}{9}=1$上一点p到两焦点距离之积为m,则m取最大值时,p点的坐标是( )
| A. | $({\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$或 $({-\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$ | B. | $({\frac{5}{2},\frac{{3\sqrt{3}}}{2}})$或$({\frac{5}{2},-\frac{{3\sqrt{3}}}{2}})$ | ||
| C. | (5,0)或(-5,0) | D. | (0,3)或(0,-3) |
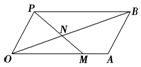 如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.
如图所示,四边形OABP是平行四边形,过点P的直线与射线OA,OB分别相交于点M,N,若$\overrightarrow{OM}$=x$\overrightarrow{OA}$,$\overrightarrow{ON}$=y$\overrightarrow{OB}$.