题目内容
14．定义在R上的偶函数y=f（x），当x≥0时，f（x）=lg（x2-3x+3），则f（x）在R上的零点个数为4个．分析 利用函数是偶函数求出xx≥0时，函数的零点个数，即可得到结果．
解答 解：当x≥0时，f（x）=lg（x2-3x+3），
函数的零点由：lg（x2-3x+3）=0，即x2-3x+3=1，解得x=1或x=2．
因为函数是定义在R上的偶函数y=f（x），所以函数的零点个数为：4个．
故答案为：4．
点评 本题考查函数的零点的个数的求法，函数的奇偶性的应用，考查计算能力．
练习册系列答案
相关题目
4．下列函数中，是偶函数且不存在零点的是（ ）
| A． | y=x2 | B． | y=$\sqrt{x}$ | C． | y=log2x | D． | y=（$\frac{1}{2}$）|x| |
19．已知函数f（x）为R上的单调函数，f-1（x）是它的反函数，点A（-1，3）和点B（1，1）均在函数f（x）的图象上，则不等式|f-1（2x）|＜1的解集为（ ）
| A． | （-1，1） | B． | （1，3） | C． | （0，log23） | D． | （1，log23） |
3．函数y=sin2x-4sinx+1的值域为（ ）
| A． | [-5，-2] | B． | [-5，6] | C． | [-2，2] | D． | [-2，6] |
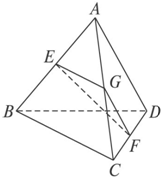如图，点A是BCD所在平面外一点，AD=BC，E、F分别是 AB、CD的中点，且EF=$\frac{{\sqrt{2}}}{2}$AD，求异面直线AD和BC所成的角．