题目内容
18.多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形.(1)求多面体ABCDEF的体积;
(2)求二面角A-BF-C的余弦值.
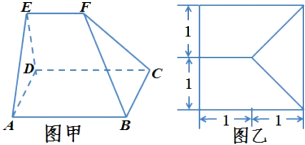
分析 (1)分别取AB、CD的中点M、N,连结EM,EN,MN,多面体体积转化为棱柱AED-MFN的体积V1和四棱锥F-MBCN的体积V2之和,由此能求出多面体ABCDEF的体积.
(2)取MN中点O,BC中点P,以OM为x轴,OP为y轴,OF为z轴,建立空间直角坐标系,利用向量法能求出二面角A-BF-C的余弦值.
解答 解:(1)分别取AB、CD的中点M、N,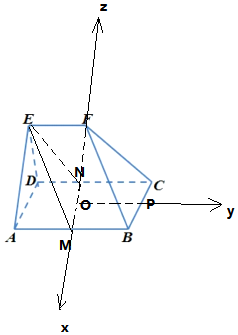
连结EM,EN,MN,
多面体体积转化为棱柱AED-MFN的体积V1和四棱锥F-MBCN的体积V2之和,
由三视图知AD=2,AM=DN=1,
又面ADE为正三角形,且垂直于底面ABCD,
∴F到底面距离为$\sqrt{3}$,
∴多面体ABCDEF的体积:
V=V1+V2=$\sqrt{3}+\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$.
(2)取MN中点O,BC中点P,
以OM为x轴,OP为y轴,OF为z轴,建立空间直角坐标系,
知A(1,-1,0),B(1,1,0),F(0,0,$\sqrt{3}$),
C(-1,1,0),
则$\overrightarrow{AB}$=(0,2,0),$\overrightarrow{AF}$=(-1,1,$\sqrt{3}$),
设平面ABF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=2y=0}\\{\overrightarrow{n}•\overrightarrow{AF}=-x+y+\sqrt{3}z=0}\end{array}\right.$,取x=$\sqrt{3}$,得$\overrightarrow{n}$=($\sqrt{3},0,1$),
同理求得平面BFC的法向量$\overrightarrow{m}$=(0,$\sqrt{3}$,1),
设二面角A-BF-C的平面角为θ,
则cosθ=-$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=-$\frac{1}{4}$.
∴二面角A-BF-C的余弦值为$\frac{1}{4}$.
点评 本题考查多面体的体积的求法,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | $({\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$或 $({-\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$ | B. | $({\frac{5}{2},\frac{{3\sqrt{3}}}{2}})$或$({\frac{5}{2},-\frac{{3\sqrt{3}}}{2}})$ | ||
| C. | (5,0)或(-5,0) | D. | (0,3)或(0,-3) |
| A. | [-5,-2] | B. | [-5,6] | C. | [-2,2] | D. | [-2,6] |
| A. | x2=2y | B. | x2=4y | C. | x2=8y | D. | x2=16y |
| A. | 2 | B. | 4 | C. | 12 | D. | 24 |