题目内容
20.已知函数$f(x)=\left\{\begin{array}{l}{log_2}({-x}),x<0\\ x-2,x≥0\end{array}\right.$,若函数g(x)=|f(x)|-a有四个不同零点x1,x2,x3,x4,且x1<x2<x3<x4,则${x_1}{x_2}{a^2}-\frac{{{x_3}+{x_4}}}{2}a+2017$的最小值为2016.分析 画出函数y=|f(x)|的图象,由题意得出a的取值范围和x1x2,x3+x4的值,再利用二次函数配方法即可求出最小值.
解答 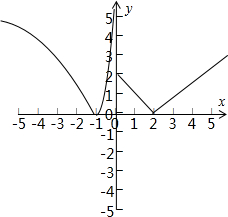 解:由题意,画出函数y=|f(x)|的图象,如图所示,
解:由题意,画出函数y=|f(x)|的图象,如图所示,
又函数g(x)=a-|f(x)|有四个零点x1,x2,x3,x4,且x1<x2<x3<x4,
所以0<a≤2,
且log2(-x1)=-log2(-x2)=2-x3=x4-2,
所以x1x2=1,x3+x4=4,
则${x_1}{x_2}{a^2}-\frac{{{x_3}+{x_4}}}{2}a+2017$
=a2-2a+2017=(a-1)2+2016,
当a=1时,取得最小值2016.
故答案为:2016.
点评 本题考查了分段函数研究函数的零点的应用问题,也考查了二次函数最值的求法与等价转化的应用问题,是综合性题目.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
11.设a、b分别是甲、乙各抛掷一枚骰子得到的点数,已知乙所得的点数为2,则方程x2+ax+b=0有两个不相等的实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{12}$ |
8.椭圆上$\frac{x^2}{25}+\frac{y^2}{9}=1$上一点p到两焦点距离之积为m,则m取最大值时,p点的坐标是( )
| A. | $({\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$或 $({-\frac{{5\sqrt{3}}}{2},\frac{3}{2}})$ | B. | $({\frac{5}{2},\frac{{3\sqrt{3}}}{2}})$或$({\frac{5}{2},-\frac{{3\sqrt{3}}}{2}})$ | ||
| C. | (5,0)或(-5,0) | D. | (0,3)或(0,-3) |