题目内容
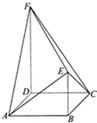 如图,多面体ABCDEF中,面ABCD为边长为a的菱形,且∠DAB=60°,DF=2BE=2a,DF∥BE,DF⊥平面ABCD
如图,多面体ABCDEF中,面ABCD为边长为a的菱形,且∠DAB=60°,DF=2BE=2a,DF∥BE,DF⊥平面ABCD(Ⅰ)在AF上是否存在点G,使得EG∥平面ABCD,请证明你的结论;
(Ⅱ)求该多面体的体积.
考点:直线与平面平行的性质,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)当点G是AF中点时,EG∥平面ABCD,证明四边形BEGH为平行四边形,可得EG∥BH,即可证明EG∥平面ABCD;
(Ⅱ)连接BD,由V=VA-BDFE+V C-BDFE=2VA-BDFE.
(Ⅱ)连接BD,由V=VA-BDFE+V C-BDFE=2VA-BDFE.
解答:
解:(Ⅰ)当点G是AF中点时,EG∥平面ABCD.
取AD中点H,连接GH,GE,BH,则
∵GH∥DF,GH=
DF,
∴GH∥BE且GH=BE,
∴四边形BEGH为平行四边形,
∴EG∥BH,
∵BH?平面ABCD,EG?平面ABCD,
∴EG∥平面ABCD;
(Ⅱ)连接BD,由V=VA-BDFE+V C-BDFE=2VA-BDFE=2•
•
(a+2a)•a•
a=
a3.
取AD中点H,连接GH,GE,BH,则
∵GH∥DF,GH=
| 1 |
| 2 |
∴GH∥BE且GH=BE,
∴四边形BEGH为平行四边形,
∴EG∥BH,
∵BH?平面ABCD,EG?平面ABCD,
∴EG∥平面ABCD;
(Ⅱ)连接BD,由V=VA-BDFE+V C-BDFE=2VA-BDFE=2•
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题考查线面平行的判定,考查多面体的体积,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
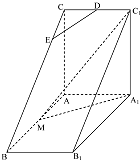 如图,直三棱柱ABC=A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点且
如图,直三棱柱ABC=A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点且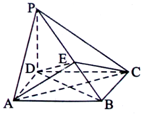 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2的菱形,∠ABC=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2的菱形,∠ABC=