题目内容
已知向量
=(2sinωx,cosωx),
=(-
sinωx,2sinωx)(ω>0)函数f(x)=
•
+
,直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,且|x1-x2|的最小值为
.
(1)求ω的值和函数f(x)的单调增区间;
(2)已知x∈[-
,θ],f(x)∈[-
,2],求θ的取值范围.
| m |
| n |
| 3 |
| m |
| n |
| 3 |
| π |
| 2 |
(1)求ω的值和函数f(x)的单调增区间;
(2)已知x∈[-
| π |
| 3 |
| 3 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(1)先根据题意表示出f(x)进而利用两角和公式和二倍角公式化简,根据题意推断出函数的周期,求得ω的值,则函数解析式可得,最后根据正弦函数的单调性求得函数的单调增区间.
(2)根据函数的值域求得x的范围,进而根据已知x的范围确定θ的范围.
(2)根据函数的值域求得x的范围,进而根据已知x的范围确定θ的范围.
解答:
解:(1)∵f(x)=-2
sin2ωx+2cosωxsinωx=sin2ωx-
(1-cos2ωx)+
=sin2ωx+
cos2ωx=2sin(2ωx+
),
又∵直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,|x1-x2|的最小值为
,
∴函数y=f(x)的最小正周期为π,
故
=π,
∴ω=1,
∴f(x)=2sin(2x+
),
由-
+2kπ≤2x+
≤
+2kπ,k∈Z,得kπ-
≤x≤kπ+
,k∈Z,
∴函数的单调增区间为[kπ-
,kπ+
](k∈Z).
(2)∵x∈[-
,θ],
∴2x+
∈[-
,2θ+
]
由f(x))∈[-
,2],
∴-
≤2sin(2x+
)≤2,
∴-
≤sin(2x+
)≤1
∴
≤x≤
,
∴
≤θ≤
.
| 3 |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
又∵直线x=x1,x=x2是函数y=f(x)的图象的任意两条对称轴,|x1-x2|的最小值为
| π |
| 2 |
∴函数y=f(x)的最小正周期为π,
故
| 2π |
| 2ω |
∴ω=1,
∴f(x)=2sin(2x+
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
∴函数的单调增区间为[kπ-
| 5π |
| 12 |
| π |
| 12 |
(2)∵x∈[-
| π |
| 3 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
由f(x))∈[-
| 3 |
∴-
| 3 |
| π |
| 3 |
∴-
| ||
| 2 |
| π |
| 3 |
∴
| π |
| 2 |
| 4π |
| 3 |
∴
| π |
| 12 |
| π |
| 2 |
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.考查了学生分析和运算的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在几何体ABCDE中,CA=CB=2,CA⊥CB,CD⊥平面ABC,F为线段AB的中点,EF∥CD,EF=CD=
如图,在几何体ABCDE中,CA=CB=2,CA⊥CB,CD⊥平面ABC,F为线段AB的中点,EF∥CD,EF=CD=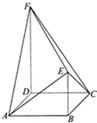 如图,多面体ABCDEF中,面ABCD为边长为a的菱形,且∠DAB=60°,DF=2BE=2a,DF∥BE,DF⊥平面ABCD
如图,多面体ABCDEF中,面ABCD为边长为a的菱形,且∠DAB=60°,DF=2BE=2a,DF∥BE,DF⊥平面ABCD