题目内容
已知定义在R上的函数f(x),满足f(x)=f(x+4),f(2+x)=f(2-x),若0<x<2时,f(x)=2-x,则f(2015)= .
考点:抽象函数及其应用
专题:函数的性质及应用
分析:由题意求出函数的周期T=4,转化f(2015)为f(4×503+3)=f(3),再由函数f(x)满足f(2+x)=f(2-x),得f(3)=f(2+1)=f(2-1)=f(1),
代入f(x)=2-x,然后求值.
代入f(x)=2-x,然后求值.
解答:
解:函数f(x)是定义在R上的函数,且满足f(x+4)=f(x),
∴函数的周期为4,f(2015)=f(4×503+3)=f(3),
函数f(x)满足f(2+x)=f(2-x),∴f(3)=f(2+1)=f(2-1)=f(1),
∵0<x<2时,f(x)=2-x,∴f(1)=2-1=
∴f(2015)=
,
故答案为:
.
∴函数的周期为4,f(2015)=f(4×503+3)=f(3),
函数f(x)满足f(2+x)=f(2-x),∴f(3)=f(2+1)=f(2-1)=f(1),
∵0<x<2时,f(x)=2-x,∴f(1)=2-1=
| 1 |
| 2 |
∴f(2015)=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:题考查函数的周期的应用,函数值的求法,考查计算能力.

练习册系列答案
相关题目
已知正六棱柱的高为6,底面边长为3,则它的体积为( )
| A、48 | ||
B、27
| ||
C、81
| ||
| D、36 |
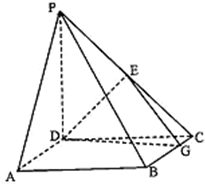 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,CB=3CG
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,CB=3CG