题目内容
如果函数f(x)=ax2+bx+c(a>0)对任意的实数x,都有f(1+x)=4f(
)成立.
(1)求
,
的值;
(2)解关于x的不等式f(x)<4a;
(3)若f(0)=1且关于α不等式f(sinα)≤sinα+m恒成立,求实数m取值范围.
| x |
| 2 |
(1)求
| b |
| a |
| c |
| a |
(2)解关于x的不等式f(x)<4a;
(3)若f(0)=1且关于α不等式f(sinα)≤sinα+m恒成立,求实数m取值范围.
考点:抽象函数及其应用,二次函数的性质
专题:函数的性质及应用
分析:(1)根据已知条件,代入得到x2+(2a+b)x+a2+b+c=ax2+2bx+4c,求出 a,b,c的值,继而求出答案.
(2)求出f(x),得到不等式,解得即可,
(3)f(sinα)≤sinα+m恒成立,即m≥sin2α+sinα+1,求出sin2α+sinα+1的最大值即可.
(2)求出f(x),得到不等式,解得即可,
(3)f(sinα)≤sinα+m恒成立,即m≥sin2α+sinα+1,求出sin2α+sinα+1的最大值即可.
解答:
解:(1)∵f(1+x)=4f(
),
∴a(x+1)2+b(x+1)+c=4[a(
x)2+b(
x)+c,
整理得,x2+(2a+b)x+a2+b+c=ax2+2bx+4c,
∴2a+b=2b,a=1,a2+b+c=4c,
解得a=1,b=2,c=1,
∴
=2,
=1;
(2)∵f(x)=ax2+bx+c,f(x)<4a;
∴ax2+bx+c<4a;
由(1)得,a=1,b=2,c=1,
∴x2+2x-3<0,
解得-3<x<1,
∴a>0时,f(x)的解集为(-3,1)
(3)由(1)得,f(x)=x2+2x+1(a>0),f(0)=1,
∵f(sinα)≤sinα+m恒成立,
∴sin2α+2sinα+1)≤sinα+m,
∴m≥sin2α+sinα+1=(sinα+
)2+
,
∵sinα∈[-1,1],
∴当sinα=1,sin2α+sinα+1有最大值,最大值为3,
∴当m≥3时不等式f(sinα)≤sinα+m恒成立,
故实数m取值范围为[3,+∞).
| x |
| 2 |
∴a(x+1)2+b(x+1)+c=4[a(
| 1 |
| 2 |
| 1 |
| 2 |
整理得,x2+(2a+b)x+a2+b+c=ax2+2bx+4c,
∴2a+b=2b,a=1,a2+b+c=4c,
解得a=1,b=2,c=1,
∴
| b |
| a |
| c |
| a |
(2)∵f(x)=ax2+bx+c,f(x)<4a;
∴ax2+bx+c<4a;
由(1)得,a=1,b=2,c=1,
∴x2+2x-3<0,
解得-3<x<1,
∴a>0时,f(x)的解集为(-3,1)
(3)由(1)得,f(x)=x2+2x+1(a>0),f(0)=1,
∵f(sinα)≤sinα+m恒成立,
∴sin2α+2sinα+1)≤sinα+m,
∴m≥sin2α+sinα+1=(sinα+
| 1 |
| 2 |
| 3 |
| 4 |
∵sinα∈[-1,1],
∴当sinα=1,sin2α+sinα+1有最大值,最大值为3,
∴当m≥3时不等式f(sinα)≤sinα+m恒成立,
故实数m取值范围为[3,+∞).
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
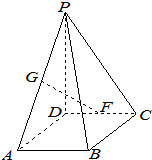 在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=
在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD= 如图,在区间(0,1]上给定曲线f(x)=x2确定t的值,使S1与S2之和最小.
如图,在区间(0,1]上给定曲线f(x)=x2确定t的值,使S1与S2之和最小.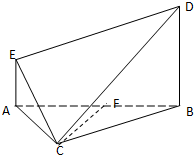 在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2
在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2