题目内容
已知∈R,函数f(x)=x2-2alnx.
(1)当a=1时,求f(x)的单调区间和最值;
(2)若a>0,试证明:“方程f(x)=2ax有唯一解”的充要条件是“a=
”.
(1)当a=1时,求f(x)的单调区间和最值;
(2)若a>0,试证明:“方程f(x)=2ax有唯一解”的充要条件是“a=
| 1 |
| 2 |
考点:利用导数研究函数的单调性,必要条件、充分条件与充要条件的判断
专题:导数的综合应用
分析:(Ⅰ)先求出f′(x)=2x-
=2•
,(x>1),再讨论(1)若a≤1,x>1,(2)若a>1,x>1的情况,从而得出结论,
(Ⅱ)记g(x)=x2-2alnx-2ax,g′(x)=
(x2-ax-a),分别证明(1)充分性(2)必要性,从而得出结论.
| 2a |
| x |
| x2-a |
| x |
(Ⅱ)记g(x)=x2-2alnx-2ax,g′(x)=
| 2 |
| x |
解答:
解:(Ⅰ)f′(x)=2x-
=2•
,(x>1),
(1)若a≤1,x>1,则f′(x)>0,
∵f(x)在[1,+∞)上连续,
∴f(x)在[1,+∞)上是单调递增函数.
∴当a≤1,x≥1时,f(x)min=f(1)=1,
(2)若a>1,x>1,令f′(x)=0,得x=
,
当x∈(1,
)时,f′(x)<0,f(x)在[1,+∞)上连续,f(x)在[1,
)上是单调递减函数.
当x∈(
,+∞)时,f′(x)>0,f(x)在[
,+∞)上是单调递增函数.
则x=
时,f(x)取得最小值.
∴当a>1,x≥1时,f(x)min=a-alna,
∴g(a)=
,
(Ⅱ)记g(x)=x2-2alnx-2ax,
g′(x)=
(x2-ax-a),
(1)充分性:若a=
,则g(x)=x2-lnx-x,
g′x)=
(2x+1)(x-1),
当x∈(0,1)时,g′(x)<0,g(x)在(0,1)上是单调递减函数;
当x∈(1,+∞)时,g′(x)>0,g(x)在(1,+∞)上是单调递增函数.
∴当x=1时,g(x)min=g(1)=0,即g(x)≥0,当且仅当x=1时取等号.
∴方程f(x)=2ax有唯一解.
(2)必要性:若方程f(x)=2ax有唯一解,即g(x)=0有唯一解.
令g′(x)=0,得x2-ax-a=0,
∵a>0,x>0,
∴x1=
(舍),x2=
,
当x∈(0,x2 )时,g′(x)<0,g(x)在(0,x2 )上是单调递减函数;
当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)上是单调递增函数.
∴当x=x2时,g′(x2)=0,g(x)min=g(x2 ),
∵g(x)=0有唯一解,∴g(x2)=0.
则
,即
,
∴2alnx2+ax2-a=0,
∵a>0,∴2lnx2+x2-1=0①,
设函数h(x)=2lnx+x-1,
∵在x>0时h(x)是增函数,∴h(x)=0至多有一解.
∵h(1)=0,∴方程①的解为x2=1,即
=1,解得a=
,
由(1)、(2)知,“方程f(x)=2ax有唯一解”的充要条件是“a=
”.
| 2a |
| x |
| x2-a |
| x |
(1)若a≤1,x>1,则f′(x)>0,
∵f(x)在[1,+∞)上连续,
∴f(x)在[1,+∞)上是单调递增函数.
∴当a≤1,x≥1时,f(x)min=f(1)=1,
(2)若a>1,x>1,令f′(x)=0,得x=
| a |
当x∈(1,
| a |
| a |
当x∈(
| a |
| a |
则x=
| a |
∴当a>1,x≥1时,f(x)min=a-alna,
∴g(a)=
|
(Ⅱ)记g(x)=x2-2alnx-2ax,
g′(x)=
| 2 |
| x |
(1)充分性:若a=
| 1 |
| 2 |
g′x)=
| 1 |
| x |
当x∈(0,1)时,g′(x)<0,g(x)在(0,1)上是单调递减函数;
当x∈(1,+∞)时,g′(x)>0,g(x)在(1,+∞)上是单调递增函数.
∴当x=1时,g(x)min=g(1)=0,即g(x)≥0,当且仅当x=1时取等号.
∴方程f(x)=2ax有唯一解.
(2)必要性:若方程f(x)=2ax有唯一解,即g(x)=0有唯一解.
令g′(x)=0,得x2-ax-a=0,
∵a>0,x>0,
∴x1=
a-
| ||
| 2 |
a+
| ||
| 2 |
当x∈(0,x2 )时,g′(x)<0,g(x)在(0,x2 )上是单调递减函数;
当x∈(x2,+∞)时,g′(x)>0,g(x)在(x2,+∞)上是单调递增函数.
∴当x=x2时,g′(x2)=0,g(x)min=g(x2 ),
∵g(x)=0有唯一解,∴g(x2)=0.
则
|
|
∴2alnx2+ax2-a=0,
∵a>0,∴2lnx2+x2-1=0①,
设函数h(x)=2lnx+x-1,
∵在x>0时h(x)是增函数,∴h(x)=0至多有一解.
∵h(1)=0,∴方程①的解为x2=1,即
a+
| ||
| 2 |
| 1 |
| 2 |
由(1)、(2)知,“方程f(x)=2ax有唯一解”的充要条件是“a=
| 1 |
| 2 |
点评:本题考察了利用导数研究函数的单调性,充分条件,必要条件的证明,本题是一道综合题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 如图,在区间(0,1]上给定曲线f(x)=x2确定t的值,使S1与S2之和最小.
如图,在区间(0,1]上给定曲线f(x)=x2确定t的值,使S1与S2之和最小.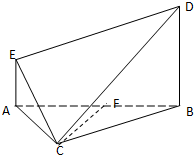 在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2
在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2