题目内容
已知F1、F2是椭圆
+
=1的两焦点,经点F2的直线交椭圆于点A、B,若|AB|=5,则|AF1|+|BF1|等于 .
| x2 |
| 16 |
| y2 |
| 9 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据A,B两点是椭圆上的两点,写出这两点与椭圆的焦点连线的线段之和等于4倍的a,根据AB的长度写出要求的结果.
解答:
解:∵直线交椭圆于点A、B,
∴由椭圆的定义可知:|AF1|+|BF1|+|AB|=4a,
∴|AF1|+|BF1|=16-5=11,
故答案为:11.
∴由椭圆的定义可知:|AF1|+|BF1|+|AB|=4a,
∴|AF1|+|BF1|=16-5=11,
故答案为:11.
点评:本题考查椭圆的基本性质和应用,解题时要注意公式的合理运用.本题主要考查了椭圆的标准方程和椭圆与其他曲线的关系.

练习册系列答案
相关题目
“a=2”是“l1:ax+4y-1=0与l2:x+ay+3=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
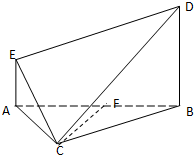 在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2
在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2