题目内容
在某医院,因为患心脏病而住院的60名男性病人中有40人秃顶;而另外50名不是因为患心脏病而住院的男性病人中有20人秃顶.求:
(1)根据题目所给的数据列出2×2列联表:
(2)能否在犯错误的概率不超过0.01的前提下认为秃顶与患心脏病有关系?(附录(1):利用随机变量公式K2=
可得观测值为k.(2)参照附表:
(1)根据题目所给的数据列出2×2列联表:
(2)能否在犯错误的概率不超过0.01的前提下认为秃顶与患心脏病有关系?(附录(1):利用随机变量公式K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)根据条件中所给的数据,列出列联表,填上对应的数据,得到列联表.
(2)假设秃顶与患心脏病没有关系,根据列联表,把求得的数据代入求观测值的公式求出观测值,把观测值同临界值进行比较得到结论.
(2)假设秃顶与患心脏病没有关系,根据列联表,把求得的数据代入求观测值的公式求出观测值,把观测值同临界值进行比较得到结论.
解答:
解:(1)根据题目所给的数据得出2×2列联表:
(2)由K2=
算得,K2=
≈7.8.
对照附表:
得,在犯错误的概率不超过0.01的前提下认为秃顶与患心脏病有关系.
| 患心脏病 | 患其他病 | 合计 | |
| 秃顶 | 40 | 20 | 60 |
| 不秃顶 | 20 | 30 | 50 |
| 合计 | 60 | 50 | 110 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 110×(40×30-20×20)2 |
| 60×50×60×50 |
对照附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
点评:本题考查独立性检验的应用,本题解题的关键是根据所给的数据填在列联表中,注意数据的位置不要出错.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
函数f(x)=x3-3x2+5的单调减区间是( )
| A、(0,2) |
| B、(0,3) |
| C、(0,1) |
| D、(0,5) |
 某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.
某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.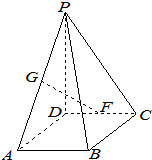 在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=
在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AB=1,BC=2,PD=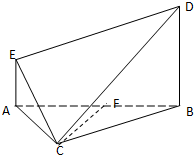 在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2
在多面体ABCDE中,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2