题目内容
10.已知随机变量ξ服从正态分布N(2,σ2),若P(ξ>-2)=0.964,则P(-2≤ξ≤6)等于0.928.分析 根据正态分布的密度函数图象关于直线x=2轴对称,即可求得P(-2≤ξ≤6).
解答 解:根据题意,正态分布N(2,σ2)的密度函数图象关于直线x=2轴对称,
∵P(ξ>-2)=0.964,
∴P(-2≤ξ≤6)=2(0.964-0.5)=0.928.
故答案为0.928.
点评 本题主要考查了正态分布曲线的特点及曲线所表示的意义,以及运用函数图象对称性解决概率问题,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
1.若向量$\overrightarrow a=(sin2α,cosα),\overrightarrow b=(1,cosα)$,且$tanα=\frac{1}{2}$,则$\overrightarrow a•\overrightarrow b$的值是( )
| A. | $\frac{8}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{4}{5}$ | D. | 2 |
18.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(0.5•{m}+1)(元)决定,其中m>0,{m}是大于或等于m的最小整数,(如:{3}=3,{3.8}=4,{3.1}=4),则从甲地到乙地通话时间为5.5分钟的电话费为( )
| A. | 3.71元 | B. | 3.97元 | C. | 4.24元 | D. | 4.77元 |
5.下列命题中,正确的一个命题是( )
| A. | “?x∈R,使得x2-1<0”的否定是:“?x∈R,均有x2-1>0” | |
| B. | “若x=3,则x2-2x-3=0”的否命题是:“若x≠3,则x2-2x-3≠0” | |
| C. | “存在四边相等的四边形不是正方形”是假命题 | |
| D. | “若cosx=cosy,则x=y”的逆否命题是真命题 |
19.圆(x+2)2+y2=2016关于直线x-y+1=0对称的圆的方程为( )
| A. | (x-2)2+y2=2016 | B. | x2+(y-2)2=2016 | C. | (x+1)2+(y+1)2=2016 | D. | (x-1)2+(y-1)2=2016 |
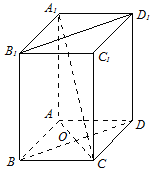 已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.
已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.