题目内容
18．拟定从甲地到乙地通话m分钟的电话费由f（m）=1.06（0.5•{m}+1）（元）决定，其中m＞0，{m}是大于或等于m的最小整数，（如：{3}=3，{3.8}=4，{3.1}=4），则从甲地到乙地通话时间为5.5分钟的电话费为（ ）| A． | 3.71元 | B． | 3.97元 | C． | 4.24元 | D． | 4.77元 |
分析 先利用{m}是大于或等于m的最小整数求出{5.5}=6，再直接代入f（m）=1.06（0.50×{m}+1）即可求出结论．
解答 解：由{m}是大于或等于m的最小整数可得{5.5}=6．
所以f（5.5）=1.06×（0.50×{5.5}+1）=1.06×4=4.24．
故选：C．
点评 本题涉及到了对新定义的考查．解决本题的关键在于对{m}是大于或等于m的最小整数的理解和应用，求出{5.5}=6．
练习册系列答案
特高级教师点拨系列答案
相关题目
8．已知离心率e=$\frac{\sqrt{5}}{2}$的双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，O为坐标原点，以OF为直径的圆与双曲线C的一条渐近线相交于O、A两点，若△AOF的面积为1，则实数a的值为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | 4 |
6．点P为棱长是2的正方体ABCD-A1B1C1D1的内切球O球面上的动点，点M为B1C1的中点，若满足DP⊥BM，则动点P的轨迹的长度为（ ）
| A． | $\frac{{\sqrt{5}π}}{5}$ | B． | $\frac{{2\sqrt{5}π}}{5}$ | C． | $\frac{{4\sqrt{5}π}}{5}$ | D． | $\frac{{8\sqrt{5}π}}{5}$ |
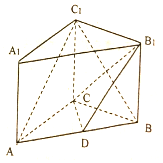如图，已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中，AC=3，AB=5，BC=4，AA1=4点D是AB的中点．
已知在长方体ABCD-A1B1C1D1中，E，M，N分别是BC，AE，D1C的中点，AD=AA1，AB=2AD．
8．函数y=ax+1（a＞0，a≠1）的图象必经过点（ ）
| A． | （0，1） | B． | （1，0） | C． | （0，2） | D． | （2，1） |