题目内容
19.圆(x+2)2+y2=2016关于直线x-y+1=0对称的圆的方程为( )| A. | (x-2)2+y2=2016 | B. | x2+(y-2)2=2016 | C. | (x+1)2+(y+1)2=2016 | D. | (x-1)2+(y-1)2=2016 |
分析 先把圆C的方程化为标准方程,求出圆心关于直线的对称点,对称后圆的半径不变,这样就可以写出对称后圆的方程.
解答 解:圆(x+2)2+y2=2016,设圆心(-2,0)关于直线x-y+1=0的对称点为(m,n)
则$\left\{\begin{array}{l}{\frac{n}{m+2}•1=-1}\\{\frac{-2+m}{2}-\frac{n}{2}+1=0}\end{array}\right.$,解得:m=-1,n=-1
∴对称点为(-1,-1)
所以圆(x+2)2+y2=2016关于直线x-y+1=0的对称圆C′的方程为:(x+1)2+(y+1)2=2016.
故选C.
点评 解决本题的关键是要明确对称后圆的位置发生了变化,圆的大小不变,只要求出圆心的对称点即可.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
8.函数y=ax+1(a>0,a≠1)的图象必经过点( )
| A. | (0,1) | B. | (1,0) | C. | (0,2) | D. | (2,1) |
9.一个年级有12个班,每个班有50名学生,随机编号为1~50,为了了解他们课外的兴趣,要求每班第40号学生留下来进行问卷调查,这运用的抽样方法是( )
| A. | 分层抽样 | B. | 抽签法 | C. | 随机数表法 | D. | 系统抽样法 |
 已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.
已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.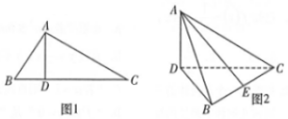 如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.