题目内容
2.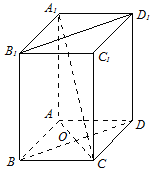 已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.
已知长方体A1B1C1D1-ABCD的高为$\sqrt{2}$,两个底面均为边长为1的正方形.(1)求证:BD∥平面A1B1C1D1;
(2)求异面直线A1C与AD所成角的大小.
分析 (1)连结B1D1,推导邮四边形B1BDD1为平行四边形,从而BD∥B1D1,由此能证明BD∥平面A1B1C1D1.
(2)由:AD∥A1D1,知∠CA1D1或其补角是A1C与AD所成角,由此能求出异面直线A1C与AD所成角.
解答 (本小题满分12分)
证明:(1)连结B1D1,∵A1B1C1D1-ABCD是长方体,
∴B1B∥D1D且B1B=D1D,
∴四边形B1BDD1为平行四边形,∴BD∥B1D1,
∵B1D1?平面A1B1C1D1,BD?平面A1B1C1D1,
∴BD∥平面A1B1C1D1.…(6分)
解:(2)由长方体的性质得:AD∥A1D1,
∴∠CA1D1或其补角是A1C与AD所成角.
连结D1C,∵A1D1⊥平面D1DCC1,∴A1D1⊥D1C,
在Rt△A1D1C中,A1D1=1,$C{D_1}=\sqrt{C{D^2}+{D_1}{D^2}}=\sqrt{3}$,
∴$tan∠CA{\;}_1{D_1}=\frac{{C{D_1}}}{{{A_1}{D_1}}}=\sqrt{3}$,∴$∠CA{\;}_1{D_1}=6{0^0}$,
即异面直线A1C与AD所成角为600.…(12分)
点评 本题考查线面平行的证明,考查异面直线所成角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
12.已知函数f(x)=mlnx+8x-x2在[1,+∞)上单调递减,则实数m的取值范围为( )
| A. | (-∞,-8] | B. | (-∞,-8) | C. | (-∞,-6] | D. | (-∞,-6) |
17.如图是一个结构图,在框②中应填入( )

| A. | 空集 | B. | 补集 | C. | 子集 | D. | 全集 |

 已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.
已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.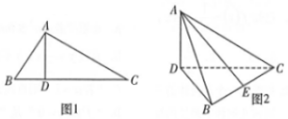 如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.
如图1,在Rt△ABC中,∠ABC=60°,AD是斜边BC上的高,沿AD将△ABC折成60°的二面角B-AD-C,如图2.