题目内容
15.已知${(3{x^2}+\sqrt{x})^n}$的展开式各项系数和为M,${(3{x^2}-\sqrt{x})^{n+5}}$的展开式各项系数和为N,(x+1)n的展开式各项的系数和为P,且M+N-P=2016,试求${(2{x^2}-\frac{1}{x^2})^{2n}}$的展开式中:(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
分析 先求出n的值,再写出展开式的通项,
(1)根据展开式的通项即可求出二项式系数最大的项,
(2)若第r+1项Tr+1的系数的绝对值最大,得到关于r的不等式组,解得即可.
解答 解:∵M+N-P=4n+2n+5-2n=(2n)2+31•2n=2016,
∴(2n)2+31•2n-2016=0,
∴(2n+63)(2n-32)=0,
∴2n=32,
∴n=5,
∴${(2{x^2}-\frac{1}{x^2})^{10}}$的展开式的通项${T_{r+1}}=C_{10}^r{(2{x^2})^{10-r}}{(-\frac{1}{x^2})^r}={(-1)^r}{2^{10-r}}C_{10}^r{x^{20-4r}}$,
(1)${(2{x^2}-\frac{1}{x^2})^{10}}$的展开式共有11项,二项式系数最大的项为中间项第6项,其值为${T_6}={(-1)^5}{2^5}C_{10}^5=-8064$,
(2)第r+1项Tr+1的系数的绝对值为${A_{r+1}}={2^{10-r}}C_{10}^r$,
若第r+1项Tr+1的系数的绝对值最大,则{$\begin{array}{l}{A_{r+1}}≥{A_r}\\{A_{r+1}}≥{A_{r+2}}\end{array}$,
可得$\frac{8}{3}≤r≤\frac{11}{3}$,又r∈N*,∴r=3,
故系数的绝对值最大的项为${T_4}={(-1)^3}{2^7}C_{10}^3{x^8}=-15360{x^8}$.
点评 本题考查二项展开式的二项式系数的性质;利用二项展开式的通项公式求展开式的特定项.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.为了研究某学科成绩是否在学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分)

(Ⅰ)求男生和女生的平均成绩
(Ⅱ)请根据图示,将2×2列联表补充完整,并根据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅲ)用分层抽样的方法从男生和女生中抽取5人进行学习问卷调查,并从5人中选取两名学生对该学科进行考后重测,求至少有一名女生的概率
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$

(Ⅰ)求男生和女生的平均成绩
(Ⅱ)请根据图示,将2×2列联表补充完整,并根据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
| 优分 | 非优分 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 50 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k2) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 0.46 | 0.71 | 1.32 | 2.07 | 2.71 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
6.点P为棱长是2的正方体ABCD-A1B1C1D1的内切球O球面上的动点,点M为B1C1的中点,若满足DP⊥BM,则动点P的轨迹的长度为( )
| A. | $\frac{{\sqrt{5}π}}{5}$ | B. | $\frac{{2\sqrt{5}π}}{5}$ | C. | $\frac{{4\sqrt{5}π}}{5}$ | D. | $\frac{{8\sqrt{5}π}}{5}$ |
20.用反证法证明命题“已知a、b、c为非零实数,且a+b+c>0,ab+bc+ca>0,求证a、b、c中至少有二个为正数”时,要做的假设是( )
| A. | a、b、c中至少有二个为负数 | B. | a、b、c中至多有一个为负数 | ||
| C. | a、b、c中至多有二个为正数 | D. | a、b、c中至多有二个为负数 |
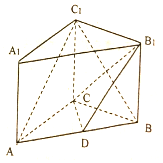 如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点.
如图,已知在侧棱垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4点D是AB的中点. 已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.
已知在长方体ABCD-A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1,AB=2AD.