题目内容
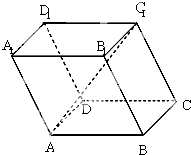已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，侧棱AA1的长为2，∠A1AB=∠A1AD=120°．（1）用基底
| AB |
| AD |
| AA1 |
| AC1 |
（2）求对角线AC1的长；
（3）求直线AC1和BB1的夹角的余弦值．
考点：平面向量数量积的运算,平面向量的基本定理及其意义
专题：计算题,空间向量及应用
分析：（1）运用向量加法的多边形法则，即可得到；
（2）运用向量的数量积的定义和向量的平方即为模的平方，即可计算得到；
（3）求出
•
的数量积，再由向量的夹角公式即可得到．
（2）运用向量的数量积的定义和向量的平方即为模的平方，即可计算得到；
（3）求出
| AC1 |
| BB1 |
解答：
解：（1）
=
+
+
=
+
+
；
（2）
•
=0，
•
=2×2×(-
)=-2，
•
=2×2×(-
)=-2，
即有|
|2=（
+
+
）2=
2+
2+
2
+2（
•
+
•
+
•
）
=4+4+4+2（0-2-2）=4，
即有|
|=2；
（3）由于
=
，
则
•
=
•
=
•
+
•
+
2=-2-2+4=0，
即有
⊥
，
故直线AC1和BB1的夹角的余弦值为0．
| AC1 |
| AB |
| BC |
| CC1 |
| AB |
| AD |
| AA1 |
（2）
| AB |
| AD |
| AB |
| AA1 |
| 1 |
| 2 |
| AD |
| AA1 |
| 1 |
| 2 |
即有|
| AC1 |
| AB |
| AD |
| AA1 |
| AB |
| AD |
| AA1 |
+2（
| AB |
| AD |
| AB |
| AA1 |
| AD |
| AA1 |
=4+4+4+2（0-2-2）=4，
即有|
| AC1 |
（3）由于
| BB1 |
| AA1 |
则
| AC1 |
| BB1 |
| AC1 |
| AA1 |
| AB |
| AA1 |
| AD |
| AA1 |
| AA1 |
即有
| AC1 |
| BB1 |
故直线AC1和BB1的夹角的余弦值为0．
点评：本题考查空间向量的数量积的定义和性质，考查向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
每课必练系列答案
相关题目
已知函数f（x）=x2，g（x）=x-1，若存在x∈R，使f（x）＜b•g（x），则b的范围是（ ）
| A、（-∞，0）∪（4，+∞） |
| B、（4，+∞） |
| C、（-∞，0） |
| D、（0，4） |